如圖1，平面直角坐標(biāo)系中，直線y=kx+b與x軸交于點(diǎn)A（6，0），與y軸交于點(diǎn)B，與直線y=2x交于點(diǎn)C（a,4）．
（1）求點(diǎn)C的坐標(biāo)及直線AB的表達(dá)式；
（2）如圖2，在x軸上有一點(diǎn)E，過(guò)點(diǎn)E作直線l⊥x軸，交直線y=2x于點(diǎn)F，交直線y=kx+b于點(diǎn)G，若GF的長(zhǎng)為3．求點(diǎn)E的坐標(biāo)；
（3）在y軸上是否存在一點(diǎn)F，使以O(shè)、C、F為頂點(diǎn)的三角形是等腰三角形，若存在，直接寫出點(diǎn)F的坐標(biāo)；若不存在，說(shuō)明理由．
【考點(diǎn)】一次函數(shù)綜合題．
【答案】（1）y=-x+6；（2）（3，0）或（1，0）；（3）存在，（0，2）或（0，-2）或（0，8）或（0，）．
5
5
5
2
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：189引用：2難度：0.2
相似題
-
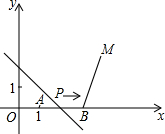1．如圖，A（1，0），B（4，0），M（5，3）．動(dòng)點(diǎn)P從點(diǎn)A出發(fā)，沿x軸以每秒1個(gè)單位長(zhǎng)的速度向右移動(dòng)，且過(guò)點(diǎn)P的直線l：y=-x+b也隨之移動(dòng)．設(shè)移動(dòng)時(shí)間為t秒．
（1）當(dāng)t=1時(shí)，求l的解析式；
（2）若l與線段BM有公共點(diǎn)，確定t的取值范圍；
（3）直接寫出t為何值時(shí)，點(diǎn)M關(guān)于l的對(duì)稱點(diǎn)落在y軸上．發(fā)布：2025/5/23 12:0:2組卷：1290引用：52難度：0.5 -
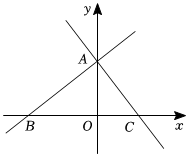2．如圖，在平面直角坐標(biāo)系中，直線y=kx+b與x軸交于點(diǎn)B（-5，0），與y軸交于點(diǎn)A，直線過(guò)點(diǎn)A，與x軸交于點(diǎn)C，點(diǎn)P是x軸上方一個(gè)動(dòng)點(diǎn)．y=-43x+4
（1）求直線AB的函數(shù)表達(dá)式；
（2）若點(diǎn)P在線段AB上，且S△APC=S△AOB，求點(diǎn)P的坐標(biāo)；
（3）當(dāng) S△PBC=S△ABC時(shí)，動(dòng)點(diǎn)M從點(diǎn)B出發(fā)，先運(yùn)動(dòng)到點(diǎn)P，再?gòu)狞c(diǎn)P運(yùn)動(dòng)到點(diǎn)C后停止運(yùn)動(dòng)．點(diǎn)M的運(yùn)動(dòng)速度始終為每秒1個(gè)單位長(zhǎng)度，運(yùn)動(dòng)的總時(shí)間為t（秒），請(qǐng)直接寫出t的最小值．發(fā)布：2025/5/22 18:30:2組卷：670引用：1難度：0.3 -
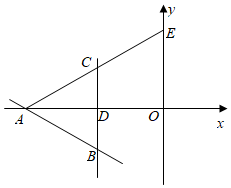3．如圖，直線y=-x-6與x軸交于點(diǎn)A，點(diǎn)B（-6，m）也在該直線上，點(diǎn)B關(guān)于x軸的對(duì)稱點(diǎn)為點(diǎn)C，直線BC交x軸于點(diǎn)D，點(diǎn)E坐標(biāo)為（0，12）．112
（1）m的值為 ，點(diǎn)C的坐標(biāo)為 ；
（2）求直線AC的函數(shù)表達(dá)式；
（3）晶晶有個(gè)想法：“設(shè)S=S△ABD+S四邊形DCEO.由點(diǎn)B與點(diǎn)C關(guān)于x軸對(duì)稱易得S△ABD=S△ACD，而△ACD與四邊形DCEO拼接后可看成△AOE，這樣求S便轉(zhuǎn)化為直接求△AOE的面積．”但經(jīng)反復(fù)演算，發(fā)現(xiàn)S△AOE≠S，請(qǐng)通過(guò)計(jì)算解釋她的想法錯(cuò)在哪里？發(fā)布：2025/5/23 2:30:1組卷：268引用：4難度：0.5