如圖1，△ABC和△ADE是等腰直角三角形，∠BAC=∠DAE=90°，點D在AC上，點E在BA延長線上，連接BD，CE．
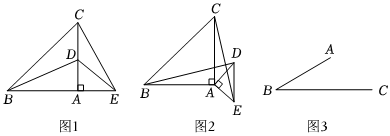
（1）線段BD與CE的數量關系是 CE=BDCE=BD；
（2）如圖2，將圖1中的△ADE繞點A順時針旋轉α（0°＜α＜90°），那么（1）問中的結論是否仍然成立？如果成立，證明你的結論，若不成立，說明理由；
（3）如圖3，若BC=5，點A是線段BC外一動點，AB=22，連接AC．若將AC繞點A逆時針旋轉90°得到AD，連接BD．則BD的最大值為 99，最小值為 11．
AB
=
2
2
【考點】幾何變換綜合題．
【答案】CE=BD；9；1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/15 8:0:9組卷：131引用：2難度：0.5
相似題
-
1．小華同學對圖形旋轉前后的線段之間、角之間的關系進行了拓展探究．
（一）猜測探究
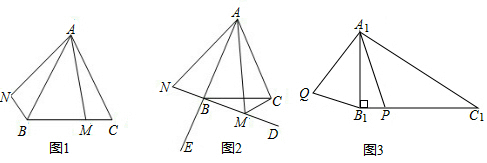
在△ABC中，AB=AC，M是平面內任意一點，將線段AM繞點A按順時針方向旋轉與∠BAC相等的角度，得到線段AN，連接NB．
（1）如圖1，若M是線段BC上的任意一點，請直接寫出∠NAB與∠MAC的數量關系是，NB與MC的數量關系是；
（2）如圖2，點E是AB延長線上點，若M是∠CBE內部射線BD上任意一點，連接MC，（1）中結論是否仍然成立？若成立，請給予證明，若不成立，請說明理由．
（二）拓展應用
如圖3，在△A1B1C1中，A1B1=8，∠A1B1C1=90°，∠C1=30°，P是B1C1上的任意點，連接A1P，將A1P繞點A1按順時針方向旋轉60°，得到線段A1Q，連接B1Q．求線段B1Q長度的最小值．發布：2025/5/30 16:30:1組卷：1725引用：4難度：0.3 -
2．如圖，等邊三角形ABC中，D為AB邊上一點（點D不與點A，B重合），連接CD，將CD平移到BE（其中點B和C對應），連接AE．將△BCD繞著點B逆時針旋轉至△BAF，延長AF交BE于點G．
（1）連接DF，求證：△BDF是等邊三角形；
（2）求證：D，F，E三點共線；
（3）當BG=2EG時，求tan∠AEB的值．發布：2025/5/30 16:30:1組卷：1311引用：6難度：0.5 -
3．閱讀與理解：如圖1，等邊△BDE按如圖所示方式設置．
操作與證明：
（1）操作：固定等邊△ABC，將△BDE繞點B按逆時針方向旋轉120°，連接AD，CE，如圖2；在圖2中，請直接寫出線段CE與AD之間具有怎樣的大小關系．
（2）操作：若將圖1中的△BDE，繞點B按逆時針方向旋轉任意一個角度α（60°＜α＜180°），連接AD，CE，AD與CE相交于點M，連BM，如圖3；在圖3中線段CE與AD之間具有怎樣的大小關系？∠EMD的度數是多少？證明你的結論．
猜想與發現：
（3）根據上面的操作過程，請你猜想在旋轉過程中，∠DMB的度數大小是否會隨著變化而變化？請證明你的結論．發布：2025/5/30 16:0:6組卷：687引用：3難度：0.4