觀察下列等式：
第一個等式：1-122=12×32；
第二個等式：1-132=23×43；
第三個等式：1-142=34×54．
按上述規律，回答下列問題：
（1）請寫出第四個等式：1-152=45×651-152=45×65；
（2）第n個等式為：1-1（n+1）2=nn+1?n+2n+11-1（n+1）2=nn+1?n+2n+1；
（3）計算：（1-122）×（1-132）×…×（1-120192）×（1-120202）．
1
-
1
2
2
=
1
2
×
3
2
1
-
1
3
2
=
2
3
×
4
3
1
-
1
4
2
=
3
4
×
5
4
1
5
2
4
5
×
6
5
1
5
2
4
5
×
6
5
1
（
n
+
1
）
2
n
n
+
1
?
n
+
2
n
+
1
1
（
n
+
1
）
2
n
n
+
1
?
n
+
2
n
+
1
（
1
-
1
2
2
）
×
（
1
-
1
3
2
）
×
…
×
（
1
-
1
2019
2
）
×
（
1
-
1
2020
2
）
【考點】規律型：數字的變化類．
【答案】1-=；1-=
1
5
2
4
5
×
6
5
1
（
n
+
1
）
2
n
n
+
1
?
n
+
2
n
+
1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：188引用：2難度：0.6
相似題
-
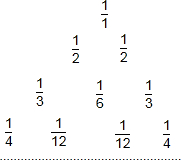1．如圖所示的數碼叫“萊布尼茨調和三角形”，它們是由整數的倒數組成的，第n行有n個數，且兩端的數均為，每個數是它下一行左右相鄰兩數的和，則第8行第3個數（從左往右數）為（ ）1n發布：2025/6/1 21:0:1組卷：3757引用：79難度：0.3 -
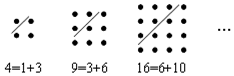2．古希臘著名的畢達哥拉斯學派把1、3、6、10 …這樣的數稱為“三角形數”，而把1、4、9、16…這樣的數稱為“正方形數”．從圖中可以發現，任何一個大于1的“正方形數”都可以看作兩個相鄰“三角形數”之和．則下列符合這一規律的等式是（ ）發布：2025/6/1 20:0:1組卷：399引用：3難度：0.7 -
3．閱讀下列材料：
因為=11×3×（1-12），13=13×5×（12-13），15=15×7×（12-15），…，17=12019×2021×12-12019，所以12021+11×3+13×5+…+15×7=12019×2021×（1-12-13+13+15-15+17+?+17-12019）=12021×（1-12）=12021．10102021
解答下列問題：
（1）在和式+11×3+13×5+…中，第5項為 ，第n項為 ，上述求和的思想方法是通過逆用異分母分數減法法則，將和式中的各分數轉化為兩個數的差，使得首末兩項外的中間各項可以 ，從而達到求和的目的；15×7
（2）利用上述結論計算：+1x（x+2）+1（x+2）（x+4）+…+1（x+4）（x+6）．1（x+2020）（x+2022）發布：2025/6/1 21:0:1組卷：161引用：1難度：0.5