為方便師生行動，我校正實施翔宇樓電梯加裝工程．我們借此構造了以下模型：已知正四棱柱ABCD-A1B1C1D1，它抽象自翔宇樓南側樓心花園所占據的空間，設AB=BC=8，AA1=12，O為底面ABCD的中心，正四棱柱OECF-O1E1C1F1與正四棱柱OECF-O2E2C2F2分別代表電梯井與電梯廂，設OO2=2，M為棱FF1的中點，N，K分別為棱AA1，DD1上的點，AN=8，DK=4．
（I）求證：OM∥平面A1CF1；
（Ⅱ）求直線A1O與平面A1CF1所成角的正弦值；
（Ⅲ）“你站在橋上看風景，看風景的人在樓上看你．明月裝飾了你的窗子，你裝飾了別人的夢．”卞之琳詩句中的情景其實正在我們的生活中反復上演，上官瑣艾同學站在樓心花園的中心（O點），她正目送著倚立在電梯廂一角的歐陽南德同學，假定上官同學的目光聚焦于棱OO2的中點I，此時，電梯廂中歐陽同學的目光正徘徊在位于N點的數學辦公室與位于K點的數學實驗室，當電梯廂向上啟動時，在這時空里便誕生了由點O與移動著的平面INK所勾勒的動人風景．現在，請作為“正在看風景的人”的你完成以下問題：當電梯廂自底部（平面OECF與平面ABCD重合）運行至頂端（平面O2E2C2F2與平面A1B1C1D1重合）的過程中，點O到平面INK距離的最大值．
【答案】（Ⅰ）證明過程見解答；
（Ⅱ）；
（Ⅲ）．
（Ⅱ）
3
11
77
（Ⅲ）
4
70
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：128引用：3難度：0.3
相似題
-
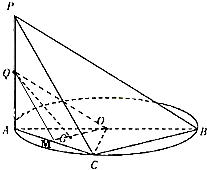1．如圖，AB是圓O的直徑，PA垂直圓O所在的平面，C是圓O上的點．
（1）求證：BC⊥平面PAC；
（2）設Q為PA的中點，G△AOC的重心，求證：QG∥平面PBC．
（3）若AC=BC=，PC與平面ACB所成的角為3，求三棱錐P-ACB的π3
體積．發布：2025/1/20 8:0:1組卷：73引用：1難度：0.7 -
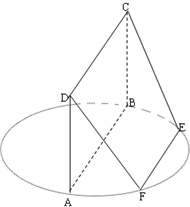2．AB為圓O的直徑，點E，F在圓上，AB∥EF，矩形ABCD所
在平面與圓O所在平面互相垂直，
已知AB=2，EF=1．
（1）求證：BF⊥平面DAF；
（2）求BF與平面ABCD所成的角；
（3）若AC與BD相交于點M，
求證：ME∥平面DAF．發布：2025/1/20 8:0:1組卷：29引用：3難度：0.1 -
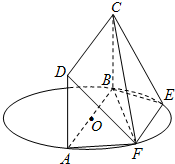3．如圖，AB為圓O的直徑，點E，F在圓上，AB∥EF，矩形ABCD所在平面與圓O所在平面互相垂直，已知AB=2，EF=1．
（Ⅰ）求證：BF⊥平面ADF；
（Ⅱ）求BF與平面ABCD所成的角；
（Ⅲ）在DB上是否存在一點M，使ME∥平面ADF？若不存在，請說明理由；若存在，請找出這一點，并證明之．發布：2025/1/20 8:0:1組卷：23引用：3難度：0.3