如圖（1）在△ABC中，∠ACB=90°，AC=BC，直線MN經(jīng)過點C，且AD⊥MN于點D，BE⊥MN于點E．
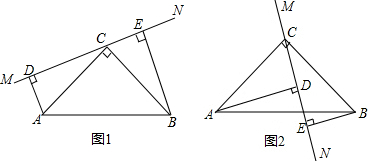
（1）求證：①△ADC≌△CEB；②DE=AD+BE．
（2）當直線MN繞點C旋轉到圖（2）的位置時，DE、AD、BE有怎樣的關系？并加以證明．
【考點】全等三角形的判定與性質；等腰直角三角形．
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：1139引用：31難度：0.3
相似題
-
1．下面是證明等腰三角形性質定理“三線合一”的三種方法，選擇其中一種完成證明．
等腰三角形性質定理：等腰三角形頂角的平分線、底邊上的中線、底邊上的高互相
重合（簡記為：三線合一）方法一：
已知：如圖，△ABC中，AB=AC，AD平分∠BAC．
求證：BD=CD，AD⊥BC．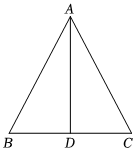
方法二：
已知：如圖，△ABC中，AB=AC，點D為BC中點．
求證：∠BAD=∠CAD，AD⊥BC．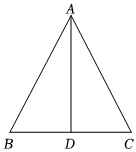
方法三：
已知：如圖，△ABC中，AB=AC，AD⊥BC．
求證：BD=CD，∠BAD=∠CAD．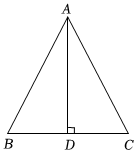
發(fā)布：2025/5/22 10:30:1組卷：261引用：2難度：0.6 -
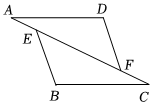2．如圖，已知AD∥BC，AD=CB，AE=CF，求證：BE=DF．發(fā)布：2025/5/22 11:0:1組卷：341引用：4難度：0.7 -
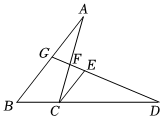3．如圖，△ABC中，D是BC延長線上一點，CD=AB，過點C作CE∥AB且CE=BC，連接DE并延長，分別交AC，AB于點F，G．
（1）求證：△ABC≌△DCE．
（2）若∠B=50°，∠D=25°，求∠AFG的度數(shù)．發(fā)布：2025/5/22 9:30:1組卷：710引用：1難度：0.5