有5名同學(xué),3男2女,現(xiàn)隨機(jī)抽2人參加課外學(xué)習(xí)小組活動(dòng),其中一定抽到女同學(xué)的概率是( )
7 10 | 3 5 | 2 5 | 3 10 |
【考點(diǎn)】列表法與樹狀圖法.
【答案】A
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2025/5/21 22:30:1組卷:114引用:5難度:0.5
相似題
-
1.某校為落實(shí)“雙減”政策,增強(qiáng)課后服務(wù)的豐富性,充分用好課后服務(wù)時(shí)間,3月份學(xué)校開展數(shù)學(xué)學(xué)科活動(dòng),其中七年級(jí)開展了五個(gè)項(xiàng)目(每位學(xué)生只能參加一個(gè)項(xiàng)目):A.閱讀數(shù)學(xué)名著;B.講述數(shù)學(xué)故事;C.制作數(shù)學(xué)模型;D.參與數(shù)學(xué)游戲;E.挑戰(zhàn)數(shù)學(xué)競(jìng)賽.為了解學(xué)生對(duì)以上活動(dòng)的參與情況,隨機(jī)抽取部分學(xué)生進(jìn)行了調(diào)查統(tǒng)計(jì),并根據(jù)統(tǒng)計(jì)結(jié)果,繪制了如圖所示的兩幅不完整的統(tǒng)計(jì)圖.
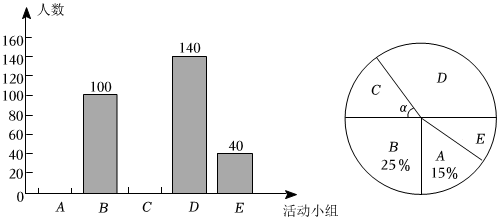
根據(jù)圖中信息,解答下列問題:
(1)①此次調(diào)查一共隨機(jī)抽取了 名學(xué)生;②補(bǔ)全條形統(tǒng)計(jì)圖(要求在條形圖上方注明名數(shù));③扇形統(tǒng)計(jì)圖中圓心角α=度;
(2)若該年級(jí)有1100名學(xué)生,請(qǐng)你估計(jì)該年級(jí)參加D項(xiàng)目的學(xué)生大約有多少名;
(3)在C項(xiàng)目展示活動(dòng)中,某班獲得一等獎(jiǎng)的學(xué)生有3名男生,2名女生,則從這5名學(xué)生中隨機(jī)抽取2名學(xué)生代表本班參加學(xué)校制作數(shù)學(xué)模型活動(dòng),請(qǐng)直接寫出恰好抽到2名男生的概率.發(fā)布:2025/5/22 4:30:1組卷:439引用:10難度:0.5 -
2.中華文化源遠(yuǎn)流長(zhǎng),文學(xué)方面,《西游記》《三國(guó)演義》《水滸傳》《紅樓夢(mèng)》是我國(guó)古代長(zhǎng)篇小說中的典型代表,被稱為“四大古典名著”.某中學(xué)為了解學(xué)生對(duì)四大名著的閱讀情況,就“四大古典名著你讀完了幾部”的問題在全校學(xué)生中進(jìn)行了抽樣調(diào)查,根據(jù)調(diào)查結(jié)果繪制成如下尚不完整的統(tǒng)計(jì)圖.
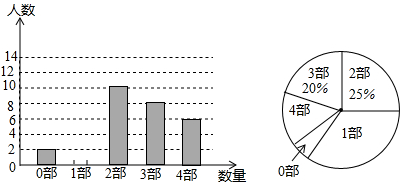
請(qǐng)根據(jù)以上信息,解決下列問題
(1)本次調(diào)查所得數(shù)據(jù)的眾數(shù)是 部,中位數(shù)是 部;
(2)扇形統(tǒng)計(jì)圖中“4部”所在扇形的圓心角為 度;
(3)請(qǐng)將條形統(tǒng)計(jì)圖補(bǔ)充完整;
(4)沒有讀過四大古典名著的兩名學(xué)生準(zhǔn)備從中各自隨機(jī)選擇一部來閱讀,求他們恰好選中同一名著的概率.發(fā)布:2025/5/22 4:0:7組卷:709引用:9難度:0.5 -
3.現(xiàn)今“微信運(yùn)動(dòng)”被越來越多的人關(guān)注和喜愛,某興趣小組隨機(jī)調(diào)查了我市部分教師某日“微信運(yùn)動(dòng)”中的步數(shù)情況進(jìn)行統(tǒng)計(jì)整理,繪制了統(tǒng)計(jì)表:
請(qǐng)根據(jù)以上信息,解答下列問題:組別 步數(shù) 頻數(shù) 頻率 1 0≤x<4000 6 a 2 4000≤x<8000 14 0.28 3 8000≤x<12000 15 b 5 12000≤x<16000 10 0.2 6 16000≤x<20000 c 0.06 7 20000≤x<24000 2 0.04
(1)本次調(diào)查的教師人數(shù)為 人,a=;
(2)這組數(shù)據(jù)的中位數(shù)落在第 組內(nèi);
(3)本市約有2000名教師,用調(diào)查的樣本數(shù)據(jù)估計(jì)日行走步數(shù)超過12000步(包含12000步)的教師有多少名?
(4)在此次調(diào)查活動(dòng)中,若從日行走步數(shù)超過16000步(包含16000步)的教師中選取兩名教師與大家分享心得,求被選取的兩名教師恰好都在20000步(包含2000步)以上的概率.發(fā)布:2025/5/22 4:0:7組卷:41引用:4難度:0.5
相關(guān)試卷


