【探究發(fā)現(xiàn)】
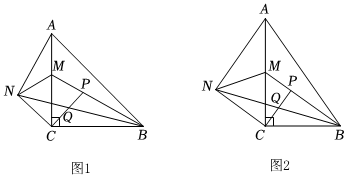
在△ABC中，∠ACB=90°，AC=BC，M是邊AC上一點(diǎn)，將△ABM沿BM折疊得到△NBM．如圖1，若BN與線段AC相交，連接AN、CN，在BM上取一點(diǎn)P，使∠BCP=∠ACN，CP交BN于點(diǎn)Q，①證明：∠NAC=∠MBC；②探究CP與CN的數(shù)量關(guān)系，并寫出探究過程；
【類比學(xué)習(xí)】
如圖2，在△ABC中，∠ACB=90°，tan∠BAC=n,M是邊AC上一點(diǎn)，將△ABM沿BM折疊得到△NBM，BN與線段AC相交，連接AN、CN，在BM上取一點(diǎn)P，使∠BCP=∠ACN，CP交BN于點(diǎn)Q，CPCN=nn（用含n的式子表示）；
【拓展應(yīng)用】
在前面的發(fā)現(xiàn)和探究的經(jīng)驗(yàn)下，當(dāng)n=22時(shí)，M是AC的中點(diǎn)時(shí)，若AN?NQ=12，求CP的長．
CP
CN
n
=
2
2
【考點(diǎn)】幾何變換綜合題．
【答案】n
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：238引用：1難度：0.1
相似題
-
1．【發(fā)現(xiàn)奧秘】
（1）如圖1，在等邊三角形ABC中，AB=2，點(diǎn)E是△ABC內(nèi)一點(diǎn)，連接AE，EC，BE，分別將AC，EC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)60°得到DC，F(xiàn)C，連接AD，DF，EF．當(dāng)B，E，F(xiàn)，D四個(gè)點(diǎn)滿足 時(shí)，BE+AE+CE的值最小，最小值為 ．
【解法探索】
（2）如圖2，在△ABC中，∠ACB=90°，AC=BC，點(diǎn)P是△ABC內(nèi)一點(diǎn)，連接PA，PB，PC，請求出當(dāng)PA+PB+PC的值最小時(shí)∠BCP的度數(shù)，并直接寫出此時(shí)PA：PB：PC的值．（提示：分別將PC，AC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)60°得到DC，EC，連接PD，DE，AE）
【拓展應(yīng)用】
（3）在△ABC中，∠ACB=90°，∠BAC=30°，BC=2，點(diǎn)P是△ABC內(nèi)一點(diǎn)，連接PA，PB，PC，直接寫出當(dāng)PA+PB+PC的值最小時(shí)，PA：PB：PC的值．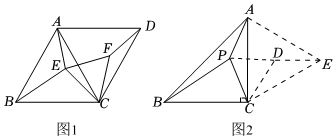
發(fā)布：2025/5/26 0:30:1組卷：232引用：1難度：0.4 -
2．下面是某數(shù)學(xué)興趣小組對一個(gè)數(shù)學(xué)問題作的探究活動(dòng)：
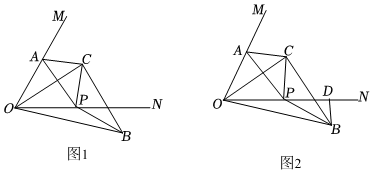
（1）如圖1，小明同學(xué)得出△OAC≌△BPC，他的判斷理由是 ．問題：
如圖1，已知，∠MON=60°，點(diǎn)A在邊OM上，點(diǎn)P是邊ON上一動(dòng)點(diǎn)，以線段AP為斜邊作Rt△ACP，AC=PC，∠ACP=90°（C和O在AP的兩側(cè)），連接OC，將線段OC繞C逆時(shí)針旋轉(zhuǎn)90°至BC，連接OB．
A．SSS
B．SAS
C．AAS
D．ASA
（2）如圖2，小穎同學(xué)作BD⊥ON于D，她認(rèn)為OA與BD存在某種數(shù)量關(guān)系，那么OA與BD是否有數(shù)量關(guān)系？如果有數(shù)量關(guān)系，請你寫出OA與BD的數(shù)量關(guān)系并說明理由；
（3）如圖1，小華說，當(dāng)OA=2，當(dāng)△AOP是直角三角形時(shí)，可求出OB2的值，請你直接寫出OB2的值．發(fā)布：2025/5/25 22:30:2組卷：142引用：2難度：0.1 -
3．如圖1，在等腰直角三角形ABC中，∠BAC=90°，點(diǎn)E，F(xiàn)分別為AB，AC的中點(diǎn)，H為線段EF上一動(dòng)點(diǎn)（不與點(diǎn)E，F(xiàn)重合），將線段AH繞點(diǎn)A逆時(shí)針方向旋轉(zhuǎn)90°得到AG，連接GC，HB．
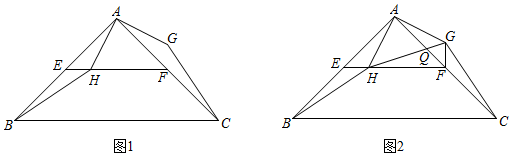
（1）證明：△AHB≌△AGC；
（2）如圖2，連接GF，HG，HG交AF于點(diǎn)Q．①證明：在點(diǎn)H的運(yùn)動(dòng)過程中，總有∠HFG=90°；②若AG=QG，AB=AC=4，求EH的長度．發(fā)布：2025/5/26 1:0:1組卷：181引用：1難度：0.3
相關(guān)試卷