如圖1，在等腰直角三角形ABC中，∠BAC=90°，點E，F分別為AB，AC的中點，H為線段EF上一動點（不與點E，F重合），將線段AH繞點A逆時針方向旋轉90°得到AG，連接GC，HB．
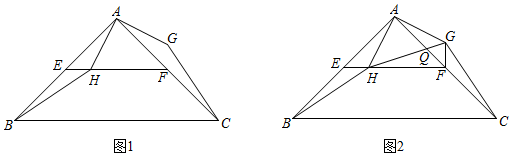
（1）證明：△AHB≌△AGC；
（2）如圖2，連接GF，HG，HG交AF于點Q．①證明：在點H的運動過程中，總有∠HFG=90°；②若AG=QG，AB=AC=4，求EH的長度．
【考點】幾何變換綜合題．
【答案】（1）證明見解答；
（2）①證明見解答；
②EH的長度2．
（2）①證明見解答；
②EH的長度2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/26 1:0:1組卷：181引用：1難度：0.3
相似題
-
1．在等腰△ABC中，∠BAC=45°，AB=AC，D是AC邊上一動點，連接BD，將BD繞點D順時針旋轉135°，得到DE，連接CE．
（1）如圖1，當點E落在BA邊的延長線上時，連接AE，BD=4，求S△BCD；2
（2）如圖2，取CE的中點F，連接DF，AF，求證：AF⊥DF；
（3）如圖3，當BD⊥AC時，點G是直線CE上一動點，連接DG，將△CDG沿著DG翻折得到△C'DG，連接AC'、BC′，若AB=4+2，請直接寫出AC′+（2-1）BC'的最小值．2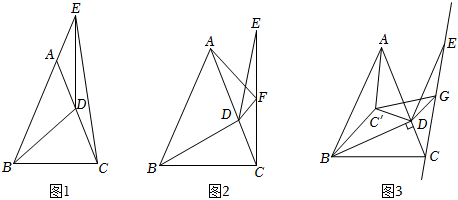
發布：2025/5/26 6:30:2組卷：268引用：1難度：0.2 -
2．已知等腰直角三角形ABC中，BC=AB，∠ABC=90°，點D在射線CB上移動（不與B、C重合），連接AD，線段AD繞點D順時針旋轉α°（0°＜α°≤180°）得到線段DE，連接CE，AE．
（1）如圖1，當點E落在線段AC上時，
①直接寫出∠BAD的度數 （可用α表示）；
②直接用等式表示CE、CD、CB的數量關系：；
（2）當點E落在線段AC的延長線上時，請在圖2中畫出符合條件的圖形，用等式表示CE、CD、CB的數量關系，并證明你的結論．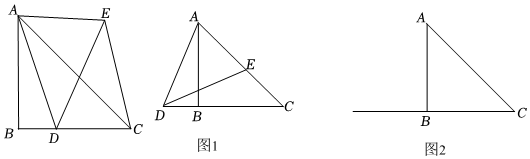
發布：2025/5/26 6:30:2組卷：317引用：3難度：0.5 -
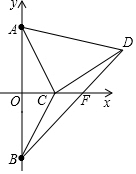3．如圖，在平面直角坐標系中，點O為坐標原點，點A（0，3）與點B關于x軸對稱，點C（n,0）為x軸的正半軸上一動點．以AC為邊作等腰直角三角形ACD，∠ACD=90°，點D在第一象限內．連接BD，交x軸于點F．
（1）如果∠OAC=38°，求∠DCF的度數；
（2）用含n的式子表示點D的坐標；
（3）在點C運動的過程中，判斷OF的長是否發生變化？若不變求出其值，若變化請說明理由．發布：2025/5/26 5:30:2組卷：556引用：5難度：0.4