如圖，由四個(gè)全等的直角三角形及一個(gè)小正方形拼成一個(gè)大正方形，已知直角三角形的短直角邊長(zhǎng)為3，小正方形的面積為1，則大正方形的面積為2525．
【考點(diǎn)】勾股定理的證明．
【答案】25
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/31 6:0:2組卷：397引用：2難度：0.7
相似題
-
1．【教材呈現(xiàn)】如圖是華師版八年級(jí)上冊(cè)124頁(yè)的部分內(nèi)容．
【證明定理】如圖，它由2個(gè)全等的直角三角形與一個(gè)小直角梯形組成，恰好拼成一個(gè)大直角梯形，也能證明勾股定理，請(qǐng)你寫(xiě)出證明過(guò)程．勾股定理的“無(wú)字證明”
在勾股定理的學(xué)習(xí)過(guò)程中，我們已經(jīng)學(xué)會(huì)了運(yùn)用以下圖形，驗(yàn)證著名的勾股定理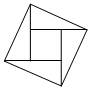
這種根據(jù)圖形直觀推論或驗(yàn)證數(shù)學(xué)規(guī)律和公式的方法，簡(jiǎn)稱為“無(wú)字證明”，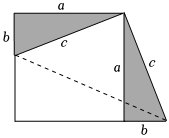
發(fā)布：2025/6/2 10:0:2組卷：466引用：1難度：0.2 -
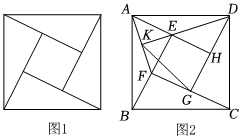2．如圖1，四個(gè)全等的直角三角形圍成一個(gè)大正方形，中間是個(gè)小正方形，這個(gè)圖形是我國(guó)漢代趙爽在注解《周髀算經(jīng)》時(shí)給出的，人們稱它為“趙爽弦圖”．在弦圖中（如圖2）連結(jié)AF，DE，并延長(zhǎng)DE交AF于點(diǎn)K，連結(jié)KG．若AH=2DH=，則KG的長(zhǎng)為（ ）22發(fā)布：2025/6/1 1:30:1組卷：531引用：5難度：0.6 -
3．我們發(fā)現(xiàn)，用不同的方式表示同一圖形的面積可以解決線段長(zhǎng)度之間關(guān)系的有關(guān)問(wèn)題，這種方法稱為等面積法，這是一種重要的數(shù)學(xué)方法，請(qǐng)你用等面積法來(lái)探究下列兩個(gè)問(wèn)題：
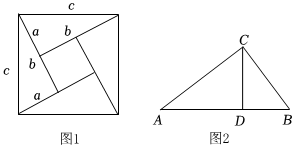
（1）如圖1是著名的“趙爽弦圖”，由四個(gè)全等的直角三角形拼成，請(qǐng)你用它驗(yàn)證勾股定理；
（2）如圖2，在Rt△ABC中∠ACB=90°，CD是AB邊上高，AC=12，BC=5，求CD的長(zhǎng)度．發(fā)布：2025/6/1 19:0:6組卷：519引用：1難度：0.6