根據閱讀材料，解決問題．
材料1：若一個正整數，從左到右各位數上的數字與從右到左各位數上的數字對應相同，則稱為“對稱數”（例如：1、232、4554是對稱數）．
材料2：對于一個三位自然數A，將它各個數位上的數字分別2倍后取個位數字，得到三個新的數字x,y,z,我們對自然數A規定一個運算：K（A）=x2+y2+z2，
例如：A=191是一個三位的“對稱數”，其各個數位上的數字分別2倍后取個位數字分別是：2、8、2．則K（191）=22+82+22=72．
請解答：
（1）請你直接寫出最大的兩位對稱數：9999，最小的三位對稱數：101101；
（2）如果將所有對稱數按照從小到大的順序排列，請直接寫出第1100個對稱數101101101101；
（3）一個四位的“對稱數”B，若K（B）=8，請求出B的所有值．
【考點】因式分解的應用．
【答案】99；101；101101
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：618引用：3難度：0.6
相似題
-
1．教科書中這樣寫道：“我們把多項式a2+2ab+b2及a2-2ab+b2叫做完全平方式”，如果一個多項式不是完全平方式，我們常做如下變形：先添加一個適當的項，使式子中出現完全平方式，再減去這個項，使整個式子的值不變，這種方法叫做配方法．配方法是一種重要的解決問題的數學方法，不僅可以將一個看似不能分解的多項式分解因式，還能解決一些與非負數有關的問題或求代數式最大值，最小值等．
例如：分解因式x2+2x-3=（x2+2x+1）-4=（x+1）2-4=（x+1+2）（x+1-2）=（x+3）（x-1）；例如求代數式2x2+4x-6的最小值.2x2+4x-6=2（x2+2x-3）=2（x+1）2-8．可知當x=-1時，2x2+4x-6有最小值，最小值是-8，根據閱讀材料用配方法解決下列問題：
（1）分解因式：m2-4m-5=．
（2）當a,b為何值時，多項式a2+b2-4a+6b+18有最小值，并求出這個最小值．
（3）當a,b為何值時，多項式a2-2ab+2b2-2a-4b+27有最小值，并求出這個最小值．發布：2025/6/22 16:30:1組卷：4095引用：9難度：0.1 -
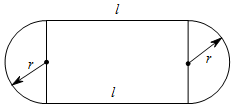2．如圖，操場的兩端為半圓形，中間是一個長方形．已知半圓的半徑為r,直跑道的長為l,請用關于r,l的多項式表示這個操場的面積．這個多項式能分解因式嗎？若能，請把它分解因式，并計算當r=40m,l=30πm時操場的面積（結果保留π）；若不能，請說明理由．發布：2025/6/22 14:30:2組卷：41引用：4難度：0.7 -
3．已知x=
+1，則代數式（x+1）2-4（x+1）+4的值是3．發布：2025/6/22 17:0:1組卷：904引用：13難度：0.7