某商家計劃在某短視頻直播平臺上直播銷售當地特產，將其中一種特產在網上進行試銷售．該商家在試銷售期間調查發現，每天銷售量y（萬件）與銷售單價x（元/件）（5≤x≤20）的數據如表：
| x（元/件） | … | 10 | 12 | 14 | 16 | … |
| y（萬件） | … | 14 | 12 | 10 | 8 | … |
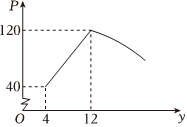
（2）總成本P（萬元）與銷售量y（萬件）之間存在如圖所示的變化趨勢，當4≤y≤12時可看成一條線段，當12≤y≤19時可看成拋物線
P
=
-
1
3
y
2
+
6
y
+
m
①銷售量不超過12萬件時，利潤為45萬元，求此時的售價為多少元/件？
②當售價為多少元時，利潤最大，最大值是多少萬元？（利潤=銷售總額-總成本）
【考點】二次函數的應用．
【答案】（1）y關于x的函數表達式為y=-x+24；
（2）①此時的售價為15或19元/件；②當售價為17元時，利潤最大，最大利潤為49萬元．
（2）①此時的售價為15或19元/件；②當售價為17元時，利潤最大，最大利潤為49萬元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/4 8:0:9組卷：469引用：2難度：0.4
相似題
-
1．為滿足市場需求，某服裝超市在六月初購進一款短袖T恤衫，每件進價是80元；超市規定每件售價不得少于90元，根據調查發現：當售價定為90元時，每周可賣出600件，一件T恤衫售價每提高1元，每周要少賣出10件．若設售價為x（x≥90）元，每周所獲利潤為Q（元），請解答下列問題：
（1）每周短袖T恤衫銷量為y（件），則y=（含x的代數式表示），并寫出Q與x的函數關系式；
（2）當售價x定為 元時，該服裝超市所獲利潤最大，最大利潤為 元；
（3）該服裝超市每周想從這款T恤衫銷售中獲利8500元，又想盡量給客戶實惠，該如何給這款T恤衫定價？發布：2025/5/23 12:30:2組卷：153引用：3難度：0.5 -
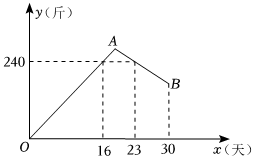2．小明家今年種植的草莓喜獲豐收，該草莓上市的成本價為10元/斤，售價為16元/斤，小明對該草莓一個月（30天）銷售情況進行記錄并繪成如圖所示的圖象．
圖中的折線OAB表示日銷量y（斤）與銷售時間x（天）之間的函數關系，若線段AB表示的函數關系中，時間每增加1天，日銷量減少20斤．
（1）第25天的日銷量是 斤，這天銷售利潤是 元；
（2）求y與x之間的函數關系式，并寫出x的取值范圍；
（3）日銷售利潤不低于1080元的天數共有多少天？銷售期間日銷售最大利潤是多少元？發布：2025/5/23 11:0:1組卷：210引用：1難度：0.4 -
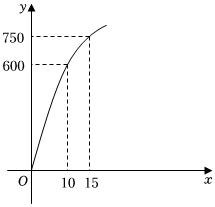3．近年來我國無人機設備發展迅猛，新型號無人機不斷面世，科研單位為保障無人機設備能安全投產，現針對某種型號的無人機的降落情況進行測試，該型號無人機在跑道起點處著陸后滑行的距離y（單位：m）與滑行時間x（單位：s）之間滿足二次函數關系，其部分函數圖象如圖所示．
（1）求y關于x的函數關系式；
（2）若跑道長度為900（m），是否夠此無人機安全著陸？請說明理由．發布：2025/5/23 13:30:1組卷：155引用：2難度：0.7