在平面直角坐標系xOy中，點A的坐標為（2，4），過（3，0）點作x軸的垂線l,點A與點B關于直線l對稱；點C的坐標為（6，0），順次連接OABC．
（1）點B的坐標為 （4，4）（4，4）；
（2）若在四邊形OABC內部有一點P，滿足S△POA=S△PBC，且S△PAB=S△POC，求點P的坐標；
（3）在四邊形OABC外部是否存在點Q，滿足S△QOA=S△QBC，且S△QAB=S△QOC，若存在，直接寫出Q點坐標，若不存在請說明理由．
【考點】四邊形綜合題．
【答案】（4，4）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/19 15:0:9組卷：118引用：1難度：0.4
相似題
-
1．【問題情境】如圖1，在△ABC中，AB=AC，點P為邊BC上的任一點，過點P作PD⊥AB，PE⊥AC，垂足分別為D、E，過點C作CF⊥AB，垂足為F．求證：PD+PE=CF．
【結論運用】如圖2，將矩形ABCD沿EF折疊，使點D落在點B上，點C落在點C'處，點P為折痕EF上的任一點，過點P作PG⊥BE、PH⊥BC，垂足分別為G、H，若AD=8，CF=3，求PG+PH的值；
【遷移拓展】如圖3，在四邊形ABCD中，∠A=∠ABC，E為AB邊上的一點，ED⊥AD，EC⊥CB，垂足分別為D、C，AB=8，AD=3，BD=7，M、N分別為AE、BE的中點，連接DM、CN，求△DEM與△CEN的周長之和．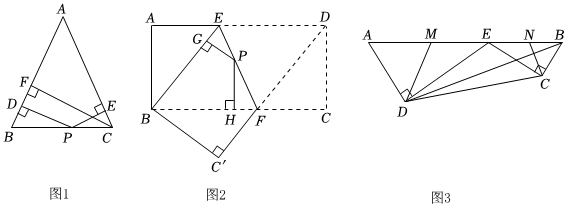
發布：2025/5/31 13:30:2組卷：319引用：2難度：0.4 -
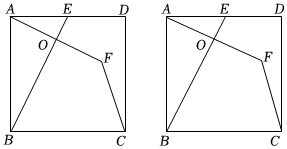2．如圖，正方形ABCD中，點E在邊AD上（不與端點A，D重合），點A關于直線BE的對稱點為點F，連接CF，設∠ABE=α．
（1）求∠AFC的大小；
（2）過點C作CG⊥AF，垂足為G，連接DG．
①求證：DG∥CF；
②連接OD，若OD⊥DG，求sinα的值．發布：2025/5/31 13:30:2組卷：1339引用：5難度：0.3 -
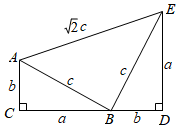3．如圖，四邊形ACDE是證明勾股定理時用到的一個圖形，a,b,c是Rt△ABC和Rt△BED邊長，易知AE=c,這時我們把關于x的形如ax2+2cx+b=0的一元二次方程稱為“勾系一元二次方程”．2
請解決下列問題：
（1）判斷下列方程是否是“勾系一元二次方程”：
①2x2+x+1=0 （填“是”或“不是”）；5
②3x2+5x+4=0 （填“是”或“不是”）2
（2）求證：關于x的“勾系一元二次方程”ax2+cx+b=0必有實數根；2
（3）若x=-1是“勾系一元二次方程”ax2+cx+b=0的一個根，且四邊形ACDE的周長是12，求△ABC面積．2發布：2025/5/31 14:0:2組卷：623引用：4難度：0.3