綜合與實踐
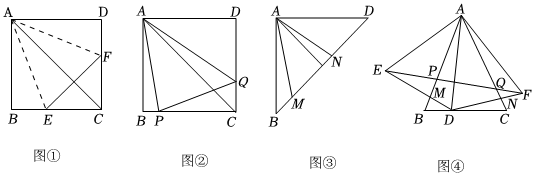
折一折：將正方形紙片ABCD折疊，使邊AB，AD都落在對角線AC上，展開得折痕AE，AF，連接EF，如圖①．
（1）∠EAF=4545°，寫出圖中兩個等腰三角形：△AEF，△EFC，△ABC，△ADC△AEF，△EFC，△ABC，△ADC（不需要添加字母）；
轉(zhuǎn)一轉(zhuǎn)：將圖①中的∠EAF繞點A旋轉(zhuǎn)．使它的兩邊分別交邊BC，CD于點P，Q，連接PQ，如圖②．
（2）線段BP，PQ，DQ之間的數(shù)量關(guān)系為 PQ=BP+DQPQ=BP+DQ；
剪一剪：將圖中的正方形紙片沿對角線BD剪開，如圖③．
（3）求證：BM2+DN2=MN2；
（4）如圖④，在等腰三角形ABC中，∠BAC=45°，AB=AC，D是BC邊上任意一點（不與點B，C重合）連接AD．以A為頂點，AD為腰向兩側(cè)分別作頂角均為45°的等腰三角形AED和等腰三角形AFD，DE，DF分別交AB，AC于點M，N，連接EF，分別交AB，AC于點P，Q．設(shè)AM=a,AB=b,則AD=abab（用a,b表示）．
ab
ab
【考點】四邊形綜合題．
【答案】45；△AEF，△EFC，△ABC，△ADC；PQ=BP+DQ；
ab
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/25 11:30:2組卷：223引用：1難度：0.2
相似題
-
1．已知，在?ABCD中，E為AB上一點，且DE=2AD，作∠ADE的平分線交AB于點F．
（1）如圖1，當E與B重合時，連接FC交BD于點G，若FC⊥CD，AF=3，求線段CF的長．
（2）如圖2，當CE⊥AB時，過點F作FH⊥BC于點H，交EC于點M．若G為FD中點，CE=2AF，求證：CD-3AG=EM．
（3）如圖3，在（1）的條件下，M為線段FC上一點，且CM=，P為線段CD上的一個動點，將線段MP繞著點M逆時針旋轉(zhuǎn)30°得到線段MP′，連接FP′，直接寫出FP′的最小值．3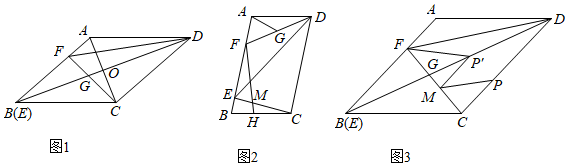
發(fā)布：2025/5/26 4:0:1組卷：481引用：2難度：0.1 -
2．如圖，△AMN是邊長為2的等邊三角形，以AN，AM所在直線為邊的平行四邊形ABCD交MN于點E、F，且∠EAF=30°．
（1）當F、M重合時，求AD的長；
（2）當NE、FM滿足什么條件時，能使；32（NE+FM）=EF
（3）在（2）的條件下，求證：四邊形ABCD是菱形．
發(fā)布：2025/5/26 2:30:2組卷：150引用：2難度：0.1 -
3．問題情境：
在數(shù)學(xué)課上，老師給出了這樣一道題：如圖1，在△ABC中，AB=AC=6，∠BAC=30°，求BC的長．
探究發(fā)現(xiàn)：
（1）如圖2，勤奮小組經(jīng)過思考后發(fā)現(xiàn)：把△ABC繞點A順時針旋轉(zhuǎn)90°得到△ADE，連接BD，BE，利用直角三角形的性質(zhì)可求BC的長，其解法如下：
過點B作BH⊥DE交DE的延長線于點H，則BC=DE=DH-HE．
△ABC繞點A順時針旋轉(zhuǎn)90°得到△ADE，AB=AC=6，∠BAC=30°∴……
請你根據(jù)勤奮小組的思路，完成求解過程．
拓展延伸：
（2）如圖3，縝密小組的同學(xué)在勤奮小組的啟發(fā)下，把△ABC繞點A順時針旋轉(zhuǎn)120°后得到△ADE，連接BD，CE交于點F，交AB于點G，請你判斷四邊形ADFC的形狀并證明；
（3）奇異小組的同學(xué)把圖3中的△BGF繞點B順時針旋轉(zhuǎn)，在旋轉(zhuǎn)過程中，連接AF，發(fā)現(xiàn)AF的長度不斷變化，直接寫出AF的最大值和最小值．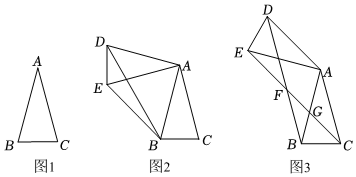
發(fā)布：2025/5/26 3:0:2組卷：83引用：1難度：0.3
相關(guān)試卷