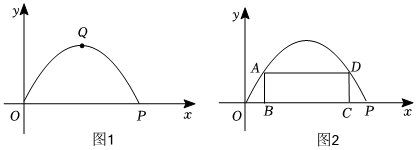
如圖1為某新建住宅小區修建的一個橫斷面為拋物線的拱形大門，點Q為頂點，其高為6米，寬OP為12米．以點O為原點，OP所在直線為x軸建立直角坐標系．
（1）求出該拋物線的函數表達式，并寫出自變量x的取值范圍；
（2）拱形大門下的道路設雙向行車道供車輛出入（正中間是寬1米的值班室），其中的一條行車道能否行駛寬2.5米、高3.5米的消防車輛？請通過計算說明；
（3）如圖2，小區物業計劃在拱形大門處安裝一個矩形“光帶”ABCD，使點A，D在拋物線上，點B，C在OP上，求出所需的三根“光帶”AB，AD，DC的長度之和的最大值．
【考點】二次函數的應用．
【答案】（1）y=-x2+2x．（0≤x≤12）；（2）能；計算過程見解析；（3）15米．
1
6
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/2 12:0:9組卷：449引用：2難度：0.6
相似題
-
1．某商場要經營一種新上市的文具，進價為20元/件，試營業階段發現：當銷售單價是25元時，每天的銷售量為250件；銷售單價每上漲1元，每天的銷售量就減少10件．
（1）請直接寫出每天銷售量y（件）與銷售單價x（元）之間的函數關系式；
（2）求出商場銷售這種文具，每天所得的銷售利潤w（元）與銷售單價x（元）之間的函數關系式（不必寫出x的取值范圍）；
（3）商場的營銷部結合實際情況，決定該文具的銷售單價不低于30元，且每天的銷售量不得少于160件，那么該文具如何定價每天的銷售利潤最大，最大利潤是多少？發布：2025/6/9 8:0:1組卷：661引用：9難度：0.5 -
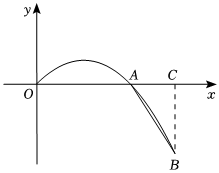2．已知某運動員在自由式滑雪大跳臺比賽中取得優異成績，為研究他從起跳至落在雪坡過程中的運動狀態，如圖，以起跳點為原點O，水平方向為x軸建立平面直角坐標系，我們研究發現他在第一次跳躍時，空中飛行的高度y（米）與水平距離x（米）具有二次函數關系，記點A為該二次函數圖象與x軸的交點，點B為該運動員的落地點，BC⊥x軸于點C．相關數據如下：OA=20米，OC=30米，tan∠BAC=．95
（1）直接寫出第一次跳躍的落地點B的坐標：；
（2）請求出第一次跳躍的高度y（米）與水平距離x（米）的二次函數解析式 ；
（3）若該運動員第二次跳躍時高度y（米）與水平距離x（米）滿足y=-0.05x2+1.1x.記他第二次跳躍時起跳點與落地點的水平距離為d米，則d 30（填“＜”、“＞”或“=”）．發布：2025/6/9 9:0:9組卷：102引用：2難度：0.4 -
3．某農作物的生長率p與溫度t（℃）有如下關系：如圖1，當10≤t≤25時可近似用函數p=
t-150刻畫；當25≤t≤37時可近似用函數p=-15（t-h）2+0.4刻畫．1160
（1）求h的值．
（2）按照經驗，該作物提前上市的天數m（天）與生長率p滿足函數關系：
①請運用已學的知識，求m關于p的函數表達式；生長率p 0.2 0.25 0.3 0.35 提前上市的天數m（天） 0 5 10 15
②請用含t的代數式表示m.
（3）天氣寒冷，大棚加溫可改變農作物生長速度．在（2）的條件下，原計劃大棚恒溫20℃時，每天的成本為200元，該作物30天后上市時，根據市場調查：每提前一天上市售出（一次售完），銷售額可增加600元．因此給大棚繼續加溫，加溫后每天成本w（元）與大棚溫度t（℃）之間的關系如圖2．問提前上市多少天時增加的利潤最大？并求這個最大利潤（農作物上市售出后大棚暫停使用）．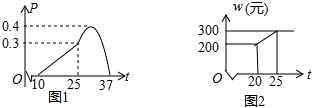
發布：2025/6/9 9:30:1組卷：2269引用：11難度：0.5