閱讀材料并回答問題:
數學課上,老師提出了如下問題:
已知點O在直線AB上,∠COE=90°,在同一平面內,過點O作射線OD,滿足∠AOC=2∠AOD.當∠BOC=40°時,如圖1所示,求∠DOE的度數.
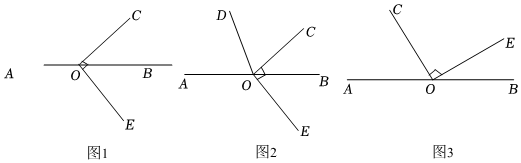
甲同學:以下是我的解答過程(部分空缺)
解:如圖2,∵點O在直線AB上,
∴∠AOB=180°.
∵∠BOC=40°,
∴∠AOC=140140°.
∵∠AOC=2∠AOD,
∴OD平分∠AOC.
∴∠COD=12∠AOC=7070°.
∵∠DOE=∠COD+∠COE,∠COE=90°,
∴∠DOE=160160°.
乙同學:“我認為還有一種情況.”
請完成以下問題:
(1)請將甲同學解答過程中空缺的部分補充完整.
(2)判斷乙同學的說法是否正確,若正確,請在圖1中畫出另一種情況對應的圖形,并求∠DOE的度數,寫出解答過程;若不正確,請說明理由.
(3)將題目中“∠BOC=40°”的條件改成“∠BOC=α”,其余條件不變,當α在90°到180°之間變化時,如圖3所示,α為何值時,∠COD=∠BOE成立?請直接寫出此時α的值.
1
2
【答案】140;70;160
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:196引用:3難度:0.4
相似題
-
 1.按要求畫圖,并回答問題:
1.按要求畫圖,并回答問題:
如圖,已知平面上四個點A,B,C,D,請按要求回答下列問題:
(1)畫直線AB,射線BD,連接AC;
(2)取線段AD中點E;
(3)請在直線AB上確定一點F,使點F到點E與點C的距離之和最短,并寫出畫圖依據(保留作圖痕跡).發布:2025/5/31 22:0:1組卷:112引用:3難度:0.6 -
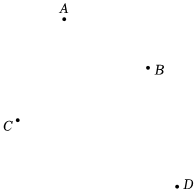 2.如圖,平面上有A、B、C、D四點,按照下列要求作答.
2.如圖,平面上有A、B、C、D四點,按照下列要求作答.
(1)畫射線CB、線段AB;
(2)連接AC,并延長至點E,使CE=AC;
(3)在射線CB上找點P,使PA+PD最小,并寫出此畫圖的依據是 .發布:2025/5/31 22:0:1組卷:40引用:1難度:0.6 -
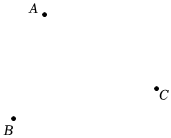 3.如圖,已知平面上有A、B、C三點,按要求進行如下操作:
3.如圖,已知平面上有A、B、C三點,按要求進行如下操作:
(1)畫出直線AB;
(2)畫出射線CA;
(3)連接BC,取BC上任一點D,連接AD.發布:2025/5/31 22:30:1組卷:7引用:1難度:0.8


