2022-2023學年廣東省梅州市五華縣興華中學七年級(下)開學數學試卷
發布:2024/4/20 14:35:0
一、單選題:本大題共10小題,每小題3分,共30分。
-
1.2020年11月24日22時06分,嫦娥五號探測器3000N發動機工作約2秒鐘,順利完成第一次軌道修正,繼續飛向月球.截至第一次軌道修正前,嫦娥五號探測器各系統狀態良好,已在軌飛行約17個小時,距離地球約16萬千米,16萬千米用科學記數法表示為( )
A.1.6×104km B.1.6×105km C.16×104km D.0.16×105km 組卷:64引用:3難度:0.8 -
2.冰箱冷藏室的溫度零上3℃,記作+3℃,則冷凍室的溫度零下17℃,記作( )
A.20℃ B.-20℃ C.17℃ D.-17℃ 組卷:52引用:3難度:0.9 -
3.若ma=mb,則下列等式不一定成立的是( )
A.a=b B.ma+3=mb+3 C.-2ma=-2mb D.ma-2=mb-2 組卷:423引用:11難度:0.9 -
4.關于-100的說法:①是有理數,②是自然數,③是整數,④是負無理數,正確個數為( )個.
A.1 B.2 C.3 D.4 組卷:73引用:3難度:0.6 -
 5.如圖,射線OA表示北偏東30°方向,射線OB表示北偏西50°方向,則∠AOB的度數是( )
5.如圖,射線OA表示北偏東30°方向,射線OB表示北偏西50°方向,則∠AOB的度數是( )A.60° B.80° C.90° D.100° 組卷:492引用:9難度:0.7 -
6.一種風箏牌面粉的質量標識為“50±0.25千克”,則下列面粉中合格的有( )
A.49.70千克 B.50.32千克 C.50.51千克 D.49.86千克 組卷:56引用:3難度:0.9 -
7.觀察下列圖形,則第2022個圖形中三角形的個數是( )
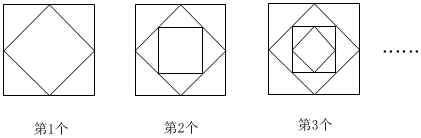
A.8084 B.8088 C.2021 D.2022 組卷:78引用:4難度:0.6 -
8.某地區居民生活用水收費標準:每月用水量不超過17立方米時,每立方米a元;超過17立方米時,超過部分每立方米(a+1.2)元.該地區某用戶上月用水量為20立方米,則應繳水費為( )
A.20a元 B.(20a+24)元 C.(17a+3.6)元 D.(20a+3.6)元 組卷:187引用:4難度:0.7
三、解答題:第18,19.20小題6分,第21,22,23小題9分,第24,25小題10分。
-
24.【新知理解】
如圖①,點C在線段AB上,若BC=πAC,則稱點C是線段AB的圓周率點,線段AC、BC稱作互為圓周率伴侶線段.
(1)若AC=3,則AB=;
(2)若點D也是圖①中線段AB的圓周率點(不同于點C),則ACBD;(填“=”或“≠”)
【解決問題】
如圖②,現有一個直徑為1個單位長度的圓片,將圓片上的某點與數軸上表示1的點重合,并把圓片沿數軸向右無滑動地滾動1周,該點到達點C的位置.
(3)若點M、N是線段OC的圓周率點,求MN的長;
(4)圖②中,若點D在射線OC上,且線段CD與以O、C、D中某兩個點為端點的線段互為圓周率伴侶線段,請直接寫出點D所表示的數.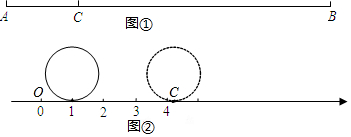 組卷:3442引用:8難度:0.3
組卷:3442引用:8難度:0.3 -
25.閱讀材料并回答問題:
數學課上,老師提出了如下問題:
已知點O在直線AB上,∠COE=90°,在同一平面內,過點O作射線OD,滿足∠AOC=2∠AOD.當∠BOC=40°時,如圖1所示,求∠DOE的度數.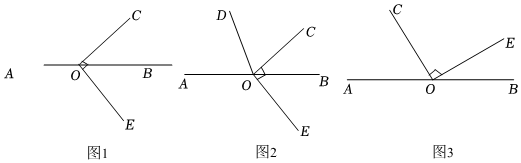
甲同學:以下是我的解答過程(部分空缺)
解:如圖2,∵點O在直線AB上,
∴∠AOB=180°.
∵∠BOC=40°,
∴∠AOC=°.
∵∠AOC=2∠AOD,
∴OD平分∠AOC.
∴∠COD=∠AOC=°.12
∵∠DOE=∠COD+∠COE,∠COE=90°,
∴∠DOE=°.
乙同學:“我認為還有一種情況.”
請完成以下問題:
(1)請將甲同學解答過程中空缺的部分補充完整.
(2)判斷乙同學的說法是否正確,若正確,請在圖1中畫出另一種情況對應的圖形,并求∠DOE的度數,寫出解答過程;若不正確,請說明理由.
(3)將題目中“∠BOC=40°”的條件改成“∠BOC=α”,其余條件不變,當α在90°到180°之間變化時,如圖3所示,α為何值時,∠COD=∠BOE成立?請直接寫出此時α的值.組卷:196引用:3難度:0.4


