九年級（3）班數學興趣小組經過市場調查整理出某種商品在第x天（1≤x≤90且x為整數）的售價與銷售量的相關信息如下．已知商品的進價為30元/件，設該商品的售價為y（單位：元/件），每天的銷售量為p（單位：件），每天的銷售利潤為w（單位：元）．
| 時間x/天 | 1 | 30 | 60 | 90 |
| 每天的銷售量p/件 | 198 | 140 | 80 | 20 |
（2）求銷售該商品第幾天時，當天的銷售利潤最大，并求出最大利潤；
（3）該商品在銷售過程中，共有多少天當天的銷售利潤不低于5600元？
【考點】二次函數的應用．
【答案】（1）每天的銷售利潤w與時間x的函數關系式是w=
；
（2）即銷售第45天時，當天的銷售利潤最大，最大利潤是6050元；
（3）該商品在銷售過程中，共有24天當天的銷售利潤不低于5600元．
- 2 x 2 + 180 x + 2000 （ 1 ≤ x ＜ 50 ） |
- 120 x + 12000 （ 50 ≤ x ≤ 90 ） |
（2）即銷售第45天時，當天的銷售利潤最大，最大利潤是6050元；
（3）該商品在銷售過程中，共有24天當天的銷售利潤不低于5600元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/21 10:30:2組卷：250引用：1難度：0.4
相似題
-
1．某超市以每件13元的價格購進一種商品，銷售時該商品的銷售單價不低于進價且不高于18元．經過市場調查發現，該商品每天的銷售量y（件）與銷售單價x（元）之間滿足如圖所示的一次函數關系．
（1）求y與x之間的函數關系式；
（2）銷售單價定為多少時，該超市每天銷售這種商品所獲的利潤最大？最大利潤是多少？發布：2025/5/21 17:0:2組卷：1871引用：12難度：0.6 -
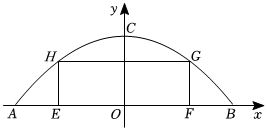2．某公園有一個拋物線形狀的觀景拱橋ABC，其橫截面如圖所示，在圖中建立的直角坐標系（以AB中點為原點，拋物線對稱軸所在直線為y軸）中，拱橋高度OC=5m,跨度AB=20m.
（1）求拋物線的解析式；
（2）拱橋下，有一加固橋身的“腳手架”矩形EFGH（H，G在拋物線上，且點H在點G的左邊），已知搭建“腳手架”EFGH的三邊所用鋼材長度為18.4m（EF在地面上，無需使用鋼材），求“腳手架”打樁點E與拱橋端點A的距離．發布：2025/5/21 16:0:1組卷：422引用：2難度：0.4 -
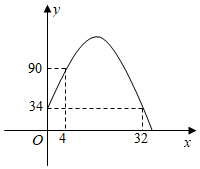3．疫情期間，按照防疫要求，學生在進校時必須排隊接受體溫檢測，某校統計了學生早晨到校情況，發現從7：00開始，在校門口的學生人數y（單位：人）隨時間x（單位：分鐘）的變化情況的圖象是二次函數圖象的一部分，如圖所示．
（1）求y與x之間的函數解析式；
（2）求校門口排隊等待體溫檢測的學生人數最多時有多少人；
（3）從7：00開始，需要多少分鐘校門口的學生才能全部進校？發布：2025/5/21 16:30:2組卷：385引用：2難度：0.4