如圖，某滑雪比賽滑道分為四段區域，運動員從助滑區AB的臺端A點出發，在助滑道AB上獲得高速度，至跳臺區BC依靠慣性配合身體動作躍向空中，從跳臺區的末端C點飛出后，身體以拋物線軌跡在空中飛行，最后落在著陸區斜坡CD上，并在終點區DE上停留等待裁判根據運動員的飛行距離和動作完美情況來評分．
已知著陸區斜坡CD的坡度均勻，CD的垂直高度CF為60m,水平距離DF為80m.某位運動員的一次動作中，在離開跳臺末端C點后水平前進了20m時，高度恰好升高了20m達到拋物線的最高點P．
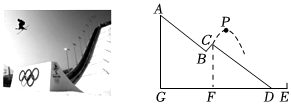
（1）請你建立合適的平面直角坐標系，并寫出拋物線的表達式；
（2）運動員在著陸區斜坡CD上著陸，可以利用斜坡的角度進行有效的緩沖，若在終點區DE上著陸，則會增加受傷風險．請你判斷這位運動員此次動作會在哪個區域著陸，并說明理由．?
【考點】二次函數的應用．
【答案】（1）平面直角坐標系見解析，拋物線的表達式為；
（2）這位運動員此次動作會在斜坡CD上著陸，理由見解析．
y
=
-
1
20
（
x
-
20
）
2
+
80
（2）這位運動員此次動作會在斜坡CD上著陸，理由見解析．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/22 15:30:1組卷：151引用：1難度：0.6
相似題
-
1．第二十四屆冬奧會在北京成功舉辦，我國選手在跳臺滑雪項目中奪得金牌．在該項目中，運動員首先沿著跳臺助滑道飛速下滑，然后在起跳點騰空，身體在空中飛行至著陸坡著陸，再滑行到停止區終止．本項目主要考核運動員的飛行距離和動作姿態，某數學興趣小組對該項目中的數學問題進行了深入研究：
如圖為該興趣小組繪制的賽道截面圖，以停止區CD所在水平線為x軸，過起跳點A與x軸垂直的直線為y軸，O為坐標原點，建立平面直角坐標系．著陸坡AC的坡角為30°，OA=65m,某運動員在A處起跳騰空后，飛行至著陸坡的B處著陸，AB=100m.在空中飛行過程中，運動員到x軸的距離y（m）與水平方向移動的距離x（m）具備二次函數關系，其解析式為y=-x2+bx+c.160
（1）求b,c的值；
（2）進一步研究發現，運動員在飛行過程中，其水平方向移動的距離x（m）與飛行時間t（s）具備一次函數關系，當運動員在起跳點騰空時，t=0，x=0；空中飛行5s后著陸．
①求x關于t的函數解析式；
②當t為何值時，運動員離著陸坡的豎直距離h最大，最大值是多少？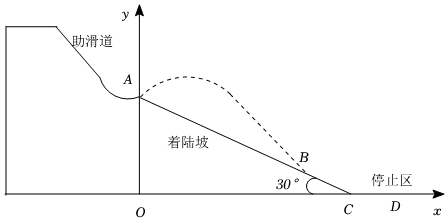
發布：2025/5/23 2:30:1組卷：2949引用：13難度：0.5 -
2．如圖1，一個移動噴灌架噴射出的水流可以近似地看成拋物線．圖2是噴灌架為一坡地草坪噴水的平面示意圖，噴水頭的高度（噴水頭距噴灌架底部的距離）是1米，當噴射出的水流與噴灌架的水平距離為10米時，達到最大高度6米，現將噴灌架置于坡地底部點O處，草坡上距離O的水平距離為15米處有一棵高度為1.2米的小樹AB，AB垂直水平地面且A點到水平地面的距離為3米．
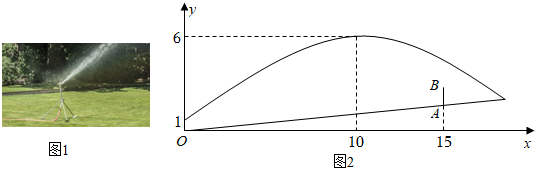
（1）計算說明水流能否澆灌到小樹后面的草地．
（2）記水流的高度為y1，斜坡的高度為y2，求y1-y2的最大值．
（3）如果要使水流恰好噴射到小樹頂端的點B，那么噴射架應向后平移多少米？發布：2025/5/23 2:30:1組卷：661引用：5難度：0.5 -
3．某產品每件成本是10元，試銷階段每件產品的售價x（元）與日銷售量y（件）之間的關系如下表：
已知日銷售量y是售價x的一次函數．x（元） 15 20 30 … y（件） 25 20 10 …
（1）求y與x的函數表達式；
（2）當銷售價為多少時，每日的銷售利潤最大？最大利潤是多少？發布：2025/5/23 2:0:6組卷：157引用：3難度：0.6