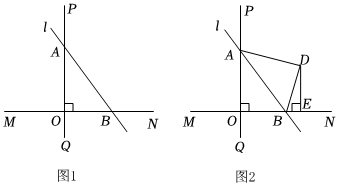
如圖1，直線MN⊥PQ，垂足為O，直線l分別與射線OP、ON相交于點(diǎn)A、B，且OA=4，OB=3，連接AB．
（1）求線段AB的長(zhǎng)；
（2）若點(diǎn)C為直線l上的一個(gè)動(dòng)點(diǎn)，求點(diǎn)O到點(diǎn)C的距離的最小值；
（3）如圖2，將△AOB沿直線l折疊，點(diǎn)O落在點(diǎn)D處，DE⊥MN，垂足為點(diǎn)E，求DE的長(zhǎng)；
（4）若點(diǎn)F為直線MN或PQ上的一個(gè)動(dòng)點(diǎn)，使得以A、B、F為頂點(diǎn)的三角形是等腰三角形，則滿足條件的所有點(diǎn)F的個(gè)數(shù)為 88個(gè)．
【考點(diǎn)】三角形綜合題．
【答案】8
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/9 0:30:2組卷：199引用：2難度：0.1
相似題
-
1．[觀察發(fā)現(xiàn)]
①如圖1，△ABC中，AB=7，AC=5，點(diǎn)D為BC的中點(diǎn)，求AD的取值范圍．
小明的解法如下：延長(zhǎng)AD到點(diǎn)E，使DE=AD，連接CE，易證△ABD≌△ECD（SAS）可得AB=CE，在△AEC中根據(jù)三角形三邊關(guān)系可得2＜AE＜12，又∵AE=2AD，∴1＜AD＜6．
②如圖2，在△ABC中，若AB=AC，則∠B=∠C；若∠B=∠C，則AB=AC．
[應(yīng)用拓展]
如圖3，∠BCA=60°，∠AED=120°，CB=CA，EA=ED，連接CD，F(xiàn)為CD的中點(diǎn)，連接FB、FE．求證：BF⊥EF．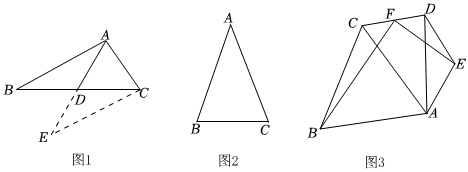
發(fā)布：2025/6/9 2:30:1組卷：109引用：2難度：0.3 -
2．下面是成成同學(xué)的數(shù)學(xué)日記，請(qǐng)你仔細(xì)閱讀，并完成相應(yīng)的任務(wù)
任務(wù)：10月20日星期四晴
今天上午第二節(jié)數(shù)學(xué)課，我們小組對(duì)“測(cè)量池塘兩岸A，B兩棵樹之間的距離”進(jìn)行了討論．
我發(fā)現(xiàn)，測(cè)量的方法特別多，現(xiàn)舉幾例，賞析如下．
明明的方法：如圖（1），在過點(diǎn)B且與AB垂直的直線l上確定一點(diǎn)D，使從點(diǎn)D可直接到達(dá)點(diǎn)A，連接AD，在AB的延長(zhǎng)線上確定一點(diǎn)C，使CD=AD，測(cè)出BC的長(zhǎng)，則AB=BC．
明明的理由：∵AD=CD，DB⊥AC，∴AB=BC．（依據(jù)1）
華華的方法：如圖（2），在地面上選取一個(gè)可以直接到達(dá)點(diǎn)A，B的點(diǎn)C，連接AC，BC，在AC，BC上分別取點(diǎn)D，E，使AD=CD，BE=CE，連接DE，測(cè)出DE的長(zhǎng)，則AB=2DE
華華的理由：∵AD=CD，BE=CE，∴DE是△ABC的中位線，∴AB=2DE．（依據(jù)2）
亮亮的方法：如圖（3），在BA的延長(zhǎng)線上取一點(diǎn)C，在過點(diǎn)C且與AB垂直的直線a上確定一點(diǎn)D，使從點(diǎn)D可直接到達(dá)點(diǎn)B，在過點(diǎn)A且與AB垂直的直線b上確定一點(diǎn)E，使點(diǎn)B，E，D在同一條直線上，測(cè)出AC，AE，CD的長(zhǎng)，即可求出AB的長(zhǎng)．
我的方法：可以在點(diǎn)A的這一邊再選定點(diǎn)C，使AC⊥AB，然后，再選定點(diǎn)E，使EC⊥AC，用視線確定AC和BE的交點(diǎn)D．此時(shí)如果測(cè)得AD、DC、EC的長(zhǎng)，就可求出A，B兩棵樹之間距離．
我感悟：知識(shí)之間是相互聯(lián)系的，同一問題可以用不同的方法來解決．我要會(huì)用“數(shù)學(xué)的眼光觀察現(xiàn)實(shí)世界，數(shù)學(xué)的思維思考現(xiàn)實(shí)世界，數(shù)學(xué)的語言表達(dá)現(xiàn)實(shí)世界，”
（1）填空：依據(jù)1指的是 ；
依據(jù)2指的是
（2）若按照亮亮的方法測(cè)出AC=10cm,AE=40m,CD=60m,請(qǐng)你求出A，B兩棵樹之間的距離．
（3）請(qǐng)你在圖（4）中，先畫出成成同學(xué)方法的示意圖，再說明理由．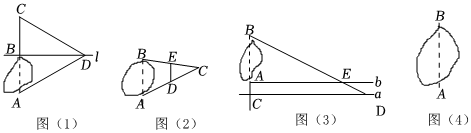
發(fā)布：2025/6/9 3:30:1組卷：69引用：1難度：0.2 -
3．【問題提出】學(xué)習(xí)了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我們繼續(xù)對(duì)“兩個(gè)三角形滿足兩邊和其中一邊的對(duì)角對(duì)應(yīng)相等”的情形進(jìn)行研究．
【初步思考】我們不妨將問題用符號(hào)語言表示為：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，對(duì)∠B進(jìn)行分類，可分為“∠B是直角、鈍角、銳角”三種情況進(jìn)行探究．
【逐步探究】
（1）第一種情況：當(dāng)∠B是直角時(shí)，如圖1，根據(jù) 定理，可得△ABC≌△DEF．
（2）第二種情況：當(dāng)∠B是鈍角時(shí)，△ABC≌△DEF仍成立．請(qǐng)你完成證明．
已知：如圖2，在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是鈍角，求證：△ABC≌△DEF．
（3）第三種情況：當(dāng)∠B是銳角時(shí)，△ABC和△DEF不一定全等．在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是銳角，請(qǐng)你用尺規(guī)在圖3中作出△DEF，使△DEF和△ABC不全等．（不寫作法，保留作圖痕跡）
【深入思考】
在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是銳角，若∠B ∠A時(shí)，則△ABC≌△DEF．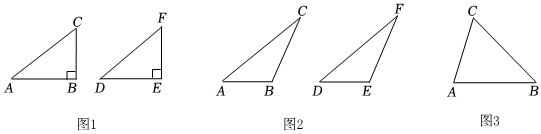
發(fā)布：2025/6/9 4:0:2組卷：248引用：2難度：0.4