如圖，在平面直角坐標系中，點O為坐標原點，在二次函數y=13x2上一點D，過D作DA⊥x軸，垂足為點A，C為y軸上一點，且OA=OC，直線CD交拋物線于第一象限一點B；
（1）若C（0，2），求直線BD的解析式；
（2）若C為y軸正半軸任意一點，連接OD，設點D的橫坐標為t,四邊形ADCO的面積為S，求S與t的關系式；
（3）如圖2，在（2）的條件下，點B關于y軸的對稱點為點E，連接BE、OE，OE交直線BD于點K，直線BD交x軸于點G，當∠FKB=2∠KBO時，求t值．
1
3
【考點】二次函數綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：67引用：1難度：0.3
相似題
-
1．如圖，拋物線y=-x+3與x軸相交于點A，B（點A在點B的左側），直線l：y=12x2+12x+b經過點A，且直線l與y軸交于點C．12
（1）求點A、B、C的坐標；
（2）點P是拋物線上的動點，過點P分別作x軸，y軸的垂線，分別與直線l交于點D、E，是否存在點P，使得△PDE與△OCA相似，且△PDE與△OCA的相似比為2：1，若存在，請求出點P的坐標，若不存在，請說明理由．發布：2025/5/23 12:30:2組卷：142引用：1難度：0.3 -
2．如圖，在平面直角坐標系中，O為坐標原點，拋物線y=ax2+bx+c與x軸交于點A、B（A左B右），與y軸交于點C，直線y=-x+3經過點B、C，AB=4．
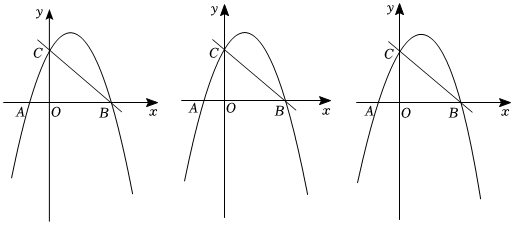
（1）求拋物線的解析式；
（2）點D在直線BC上方的拋物線上，過點D作x軸的垂線，垂足為F，交BC于點E，DE=2EF，求點D的坐標；
（3）在（2）的條件下，點G在點B右側x軸上，連接CG，AC，，過點G作GP⊥x軸交拋物線于點P，連接BP，點H在y軸負半軸上，連接HF，若∠OHF+∠GPB=45°，連接DH，求直線DH的解析式．∠ACO=12∠AGC發布：2025/5/23 12:30:2組卷：170引用：1難度：0.3 -
3．如圖，拋物線y=x2+bx+c與x軸交于A，B兩點，點A，B分別位于原點的左、右兩側，BO=3AO=3，過點B的直線與y軸正半軸和拋物線的交點分別為C，D，BC=3+36CD．3
（1）求b,c的值；
（2）求直線BD的函數解析式；
（3）點P在拋物線的對稱軸上且在x軸下方，點Q在射線BA上．當△ABD與△BPQ相似時，請直接寫出所有滿足條件的點Q的坐標．發布：2025/5/23 12:30:2組卷：5670引用：5難度：0.2