如圖1，等邊△ABC中，AD是BC邊上的中線，E為AD上一點(diǎn)（點(diǎn)E與點(diǎn)A不重合），以CE為一邊且在CE下方作等邊△CEF，連接BF．
（1）猜想線段AE，BF的數(shù)量關(guān)系：AE=BFAE=BF（不必證明）；
（2）當(dāng)點(diǎn)E為AD延長(zhǎng)線上一點(diǎn)時(shí)，其它條件不變．
①請(qǐng)你在圖2中補(bǔ)全圖形；
②（1）中結(jié)論成立嗎？若成立，請(qǐng)證明；若不成立請(qǐng)說(shuō)明理由．
【考點(diǎn)】三角形綜合題．
【答案】AE=BF
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：129引用：3難度：0.4
相似題
-
1．[觀察發(fā)現(xiàn)]
①如圖1，△ABC中，AB=7，AC=5，點(diǎn)D為BC的中點(diǎn)，求AD的取值范圍．
小明的解法如下：延長(zhǎng)AD到點(diǎn)E，使DE=AD，連接CE，易證△ABD≌△ECD（SAS）可得AB=CE，在△AEC中根據(jù)三角形三邊關(guān)系可得2＜AE＜12，又∵AE=2AD，∴1＜AD＜6．
②如圖2，在△ABC中，若AB=AC，則∠B=∠C；若∠B=∠C，則AB=AC．
[應(yīng)用拓展]
如圖3，∠BCA=60°，∠AED=120°，CB=CA，EA=ED，連接CD，F(xiàn)為CD的中點(diǎn)，連接FB、FE．求證：BF⊥EF．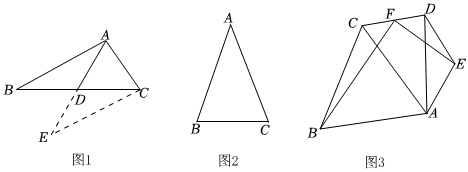
發(fā)布：2025/6/9 2:30:1組卷：109引用：2難度：0.3 -
2．已知，在平面直角坐標(biāo)系中，A（a,0），B（b,0）為x軸上兩點(diǎn)，且a,b滿足：（a+3）2+（a+b）2=0，點(diǎn)C（0，
），∠ABC=30°，D為線段AB上一動(dòng)點(diǎn)．3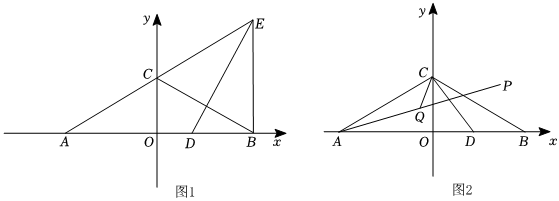
（1）則a=，b=．
（2）如圖1，若點(diǎn)D在BC的垂直平分線上，作∠ADE=120°，交AC的延長(zhǎng)線于點(diǎn)E，連接BE，求證：BE⊥x軸；
（3）如圖2，作點(diǎn)D關(guān)于BC的對(duì)稱(chēng)點(diǎn)P，連接AP，取AP中點(diǎn)Q，連接CQ、CD，求CQ的最小值．發(fā)布：2025/6/9 2:0:7組卷：263引用：1難度：0.4 -
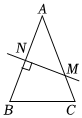3．如圖，在△ABC中，AB=AC，AB的垂直平分線交AB于N，交AC于M．
（1）若∠B=70°，則∠NMA的度數(shù)是 °．
（2）連接MB，若AB=8cm,△MBC的周長(zhǎng)是14cm.
①求BC的長(zhǎng)；
②點(diǎn)Q是線段BC上的動(dòng)點(diǎn)，在直線MN上是否存在點(diǎn)P，使由BP+PQ最小？若存在，求BP+PQ的最小值；若不存在，說(shuō)明理由．發(fā)布：2025/6/9 2:30:1組卷：27引用：1難度：0.3