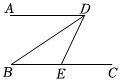
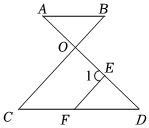
如圖,直線AC∥BD,連接AB,直線AC、BD及線段AB把平面分成①、②、③、④四個部分,規定:線上各點不屬于任何部分.當動點P落在某個部分時,連接PA,PB,構成∠PAC,∠APB,∠PBD三個角.(提示:有公共端點的兩條重合的射線所組成的角是0°角)
(1)當動點P落在第①部分時,∠APB、∠PAC、∠PBD之間滿足怎樣的數量關系?并加以證明;
(2)當動點P落在第②部分時,∠APB、∠PAC、∠PBD之間又滿足怎樣的數量關系?并加以證明;
(3)當動點P落在第③部分時且在直線AB右側時,∠PAC,∠APB,∠PBD之間又滿足怎樣的關系,直接寫出最后的結論.

【考點】平行線的性質.
【答案】(1)∠APB=∠PAC+∠PBD,理由見解答;
(2)∠APB+∠PAC+∠PBD=360°,理由見解答;
(3)∠PAC=∠PBD-∠APB,理由見解答.
(2)∠APB+∠PAC+∠PBD=360°,理由見解答;
(3)∠PAC=∠PBD-∠APB,理由見解答.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/7/6 8:0:9組卷:130引用:1難度:0.5