在同一平面內有2000條直線m1，m2…，m2000，如m1⊥m2，m2∥m3，m3⊥m4，m4∥m5，…，則m1與m2000的位置關系是 m1∥m2000m1∥m2000．
【考點】平行線的性質；規律型：圖形的變化類．
【答案】m1∥m2000
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 18:30:1組卷：4引用：1難度：0.5
相似題
-
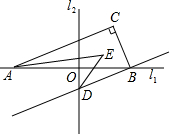1．如圖，直線l1⊥直線l2，垂足為O，Rt△ABC如圖放置，過點B作BD∥AC交直線l2于點D，在△ABC內取一點E，連接AE，DE．
（1）若∠CAE=15°，∠EDB=25°，則∠AED=．
（2）若∠EAC=∠CAB，∠EDB=1n∠ODB，則∠AED=°．（用含n的代數式表示）1n發布：2025/6/5 14:30:1組卷：1508引用：7難度：0.5 -
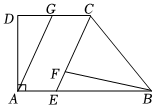2．如圖，在四邊形ABCD中，AB∥CD，∠BAD=90°，CE平分∠BCD，∠CBF=6∠EBF，AG∥CE，點H在直線CE上，滿足∠FBH=∠DAG，若∠DAG=k∠EBH，則k=（ ）發布：2025/6/5 14:30:1組卷：259引用：9難度：0.4 -
3．如圖，直線AC∥BD，連接AB，直線AC，BD及線段AB把平面分成①，②，③，④四個部分，當動點P落在某個部分時，連接PA，PB，構成∠PAC，∠APB，∠PBD三個角．（規定：線上各點不屬于任何部分且點P，A，B三點不共線）
（1）當動點P落在第①部分時，求證：∠APB=∠PAC+∠PBD；
（2）當動點P落在第②部分時，直接用等式表示∠PAC，∠APB，∠PBD之間的數量關系；
（3）當動點P落在第③部分時，用等式表示∠PAC，∠APB，∠PBD之間的數量關系，并寫出動點P的具體位置和相應的結論，選擇其中一種結論加以證明．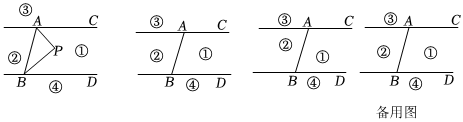
?發布：2025/6/5 14:30:1組卷：768引用：2難度：0.1