對于⊙C和⊙C上的一點A，若平面內(nèi)的點P滿足：射線AP與⊙C交于點Q（點Q可以與點P重合），且1≤PAQA≤2，則點P稱為點A關(guān)于⊙C的“生長點”．
已知點O為坐標(biāo)原點，⊙O的半徑為1，點A（-1，0）．
（1）若點P是點A關(guān)于⊙O的“生長點”，且點P在x軸上，請寫出一個符合條件的點P的坐標(biāo) （2，0）（答案不唯一）（2，0）（答案不唯一）；
（2）若點B是點A關(guān)于⊙O的“生長點”，且滿足∠BAO=30°，求點B的縱坐標(biāo)t的取值范圍；
（3）直線y=3x+b與x軸交于點M，且與y軸交于點N，若線段MN上存在點A關(guān)于⊙O的“生長點”，直接寫出b的取值范圍是 -4-3≤b≤-1或1≤b≤4-3-4-3≤b≤-1或1≤b≤4-3．
PA
QA
3
3
3
3
3
【考點】圓的綜合題．
【答案】（2，0）（答案不唯一）；-4-≤b≤-1或1≤b≤4-
3
3
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：399引用：1難度：0.1
相似題
-
1．小銳同學(xué)是一個數(shù)學(xué)學(xué)習(xí)愛好者，他在一本數(shù)學(xué)課外讀物上看到一個課本上沒有的與圓相關(guān)的角--弦切角（弦切角的定義：把頂點在圓上，一邊與圓相切，另一邊和圓相交的角叫做弦切角），并嘗試用所學(xué)的知識研究弦切角的有關(guān)性質(zhì)．
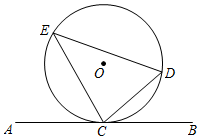
（1）如圖，直線AB與⊙O相切于C點，D，E為⊙O上不同于C的兩點，連接CE，DE，CD．請你寫出圖中的兩個弦切角 ；（不添加新的字母和線段）
（2）小銳目測∠DCB和∠DEC可能相等，并通過測量的方法驗證了他的結(jié)論，你能幫小銳用幾何推理的方法證明結(jié)論的正確性嗎？已知：如圖，直線AB ，D，E為圓上不同于C的兩點，連接CE，DE，CD．求證：．
（3）如果我們把上述結(jié)論稱為弦切角定理，請你用一句話概括弦切角定理 ．發(fā)布：2025/6/16 22:30:4組卷：176引用：2難度：0.5 -
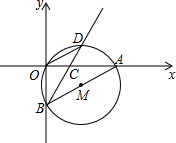2．如圖，在直角坐標(biāo)系中，⊙M經(jīng)過原點O（0，0），點A（，0）與點B（0，-6），點D在劣弧2上，連接BD交x軸于點C，且∠COD=∠CBO．?OA
（1）求⊙M的半徑；
（2）求證：BD平分∠ABO；
（3）在線段BD的延長線上找一點E，使得直線AE恰好為⊙M的切線，求此時點E的坐標(biāo)．發(fā)布：2025/6/16 21:30:2組卷：3474引用：15難度：0.1 -
3．如圖，直角坐標(biāo)系中，直線y=kx+b分別交x,y軸于點A（-8，0），B（0，6），C（m,0）是射線AO上一動點，⊙P過B，O，C三點，交直線AB于點D（B，D不重合）．
（1）求直線AB的函數(shù)表達式．
（2）若點D在第一象限，且tan∠ODC=，求點D的坐標(biāo)．53
（3）當(dāng)△ODC為等腰三角形時，求出所有符合條件的m的值．
（4）點P，Q關(guān)于OD成軸對稱，當(dāng)點Q恰好落在直線AB上時，直接寫出此時BQ的長．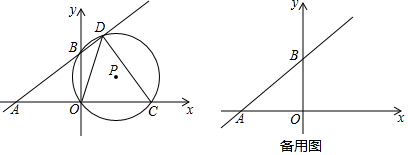
發(fā)布：2025/6/16 6:0:1組卷：324引用：5難度：0.1