小銳同學是一個數學學習愛好者，他在一本數學課外讀物上看到一個課本上沒有的與圓相關的角--弦切角（弦切角的定義：把頂點在圓上，一邊與圓相切，另一邊和圓相交的角叫做弦切角），并嘗試用所學的知識研究弦切角的有關性質．
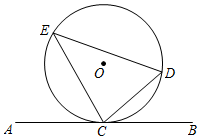
（1）如圖，直線AB與⊙O相切于C點，D，E為⊙O上不同于C的兩點，連接CE，DE，CD．請你寫出圖中的兩個弦切角 ∠ACE和∠BCD∠ACE和∠BCD；（不添加新的字母和線段）
（2）小銳目測∠DCB和∠DEC可能相等，并通過測量的方法驗證了他的結論，你能幫小銳用幾何推理的方法證明結論的正確性嗎？已知：如圖，直線AB 與⊙O相切于點C與⊙O相切于點C，D，E為圓上不同于C的兩點，連接CE，DE，CD．求證：∠DCB=∠DEC∠DCB=∠DEC．
（3）如果我們把上述結論稱為弦切角定理，請你用一句話概括弦切角定理 弦切角等于其兩邊所夾弧對的圓周角弦切角等于其兩邊所夾弧對的圓周角．
【考點】圓的綜合題．
【答案】∠ACE和∠BCD；與⊙O相切于點C；∠DCB=∠DEC；弦切角等于其兩邊所夾弧對的圓周角
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：176引用：2難度：0.5
相似題
-
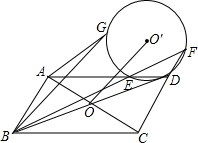1．如圖，已知四邊形ABCD是平行四邊形，AC，BD相交于O，∠ABC的平分線交CD的延長線于F，⊙O′是△DEF的外接圓，G是⊙O上一點，且AG=CD．求證：BG∥OO′．發布：2025/5/27 11:30:1組卷：82引用：1難度：0.5 -
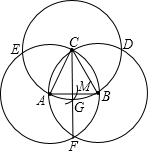2．如圖，分別以邊長1為的等邊三角形ABC的頂點為圓心，以其邊長為半徑作三個等圓，得交點D、E、F，連接CF交⊙C于點G，以點E為圓心，EG長為半徑畫弧，交邊AB于點M，求AM的長．發布：2025/5/27 4:30:2組卷：57引用：1難度：0.5 -
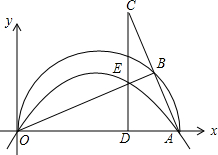3．如圖，在平面直角坐標系中，A（10，0），以OA為直徑在第一象限內作半圓，B為半圓上一點，連接AB并延長至C，使BC=AB，過C作CD⊥x軸于點D，交線段OB于點E．已知CD=8，拋物線經過O，E，A三點．
（1）求直線OB的函數表達式；
（2）求拋物線的函數表達式；
（3）若P為拋物線上位于第一象限內的一個動點，以P，O，A，E為頂點的四邊形面積記作S，則S取何值時，相應的點P有且只有3個．發布：2025/5/26 19:30:1組卷：111引用：1難度：0.3