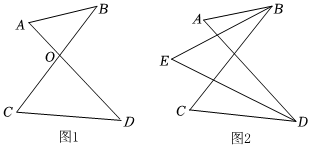
“8字”的性質及應用：
（1）如圖1，AD，BC相交于點O，得到一個“8字”ABCD，試說明∠A+∠B=∠C+∠D的理由；
（2）如圖2，以圖中給的字母為頂點的“8字”有多少個；
（3）如圖2，∠ABC和∠ADC的平分線相交于點E，利用（1）中的結論試說明∠E=12（∠A+∠C）的理由．
1
2
【考點】三角形內角和定理．
【答案】（1）證明見解答；
（2）3個；
（3）證明見解答．
（2）3個；
（3）證明見解答．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/18 5:0:1組卷：709引用：3難度：0.5
相似題
-
1．【數學模型】
如圖（1），AD，BC交于O點，根據“三角形內角和是180°”，不難得出兩個三角形中的角存在以下關系：①∠DOC=∠AOB；②∠D+∠C=∠A+∠B．
【提出問題】
分別作出∠BAD和∠BCD的平分線，兩條角平分線交于點E，如圖（2），∠E與∠D、∠B之間是否存在某種數量關系呢？
【解決問題】
為了解決上面的問題，我們先從幾個特殊情況開始探究．已知∠BAD的平分線與∠BCD的平分線交于點E．
（1）如圖（3），若AB∥CD，∠D=30°，∠B=40°，則∠E=．
（2）如圖（4），若AB不平行CD，∠D=30°，∠B=50°，則∠E的度數是多少呢？
易證∠D+∠1=∠E+∠3，∠B+∠4=∠E+∠2，請你完成接下來的推理過程：
∴∠D+∠1+∠B+∠4=，
∵CE、AE分別是∠BCD、∠BAD的平分線，
∴∠1=∠2，∠3=∠4．
∴2∠E=，
又∵∠D=30°，∠B=50°，
∴∠E=度．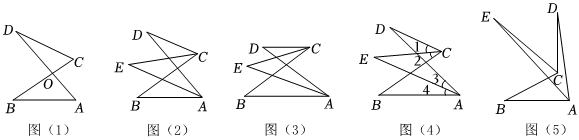
（3）在總結前兩問的基礎上，借助圖（2），直接寫出∠E與∠D、∠B之間的數量關系是：．
【類比應用】
如圖（5），∠BAD的平分線AE與∠BCD的平分線CE交于點E．
已知：∠D=α、∠B=β，（α＜β）則∠E=（用α、β表示）．發布：2025/6/3 0:0:1組卷：2583引用：4難度：0.3 -
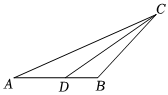2．如圖，在△ABC中，∠A=28°，∠ABC=120°，CD是△ABC的角平分線．
（1）CE是AB邊上的高線，請畫出圖形；
（2）在（1）條件下，求∠DCE的度數．發布：2025/6/2 22:0:1組卷：209引用：3難度：0.6 -
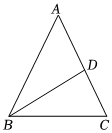3．如圖，在△ABC中，∠A=40°，∠ABC=70°，BD平分∠ABC，則∠BDC的度數是 度．發布：2025/6/2 22:0:1組卷：11引用：2難度：0.7