古希臘數(shù)學(xué)家畢達(dá)哥拉斯認(rèn)為：“一切平面圖形中最美的是圓”，它的完美來自對稱．其中切弦（chord of contact）亦稱切點(diǎn)弦，是一條特殊弦，從圓外一點(diǎn)向圓引兩條切線，連接這兩個切點(diǎn)的弦稱為切弦．此時，圓心與已知點(diǎn)的連線垂直平分切弦．
（1）為了說明切弦性質(zhì)的正確性，需要對其進(jìn)行證明．如下給出了不完整的“已知”和“求證”，請補(bǔ)充完整，并寫出“證明”過程．
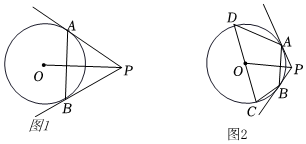
已知：如圖1，P是⊙O外一點(diǎn)，PA、PB與⊙O分別相切于點(diǎn)A、B，連接AB，OP，PA、PB與⊙O分別相切于點(diǎn)A、B，連接AB，OP，．
求證：OP垂直平分ABOP垂直平分AB．
（2）如圖2，在（1）的條件下，CD是⊙O的直徑，連接AD，BC，若∠ADC=50°，∠BCD=70°，OC=2，求OP的長．
【答案】PA、PB與⊙O分別相切于點(diǎn)A、B，連接AB，OP，；OP垂直平分AB
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/22 9:30:1組卷：505引用：5難度：0.5
相似題
-
1．如圖是吊車在吊一物品時的示意圖，已知吊車底盤CD的高度為2米，支架BC的長為4米，且與地面成30°角，吊繩AB與支架BC的夾角為80°，吊臂AC與地面成70°角，求吊車的吊臂頂端A點(diǎn)距地面的高度是多少米？（精確到0.1米）
（參考數(shù)據(jù)：sin10°=cos80°=0.17，cos10°=sin80°=0.98，sin20°=cos70°=0.34，tan70°=2.75，sin70°=0.94）發(fā)布：2025/6/25 0:0:1組卷：1604引用：53難度：0.5 -
2．北京時間2015年04月25日14時11分，尼泊爾發(fā)生8.1級強(qiáng)烈地震，我國積極組織搶險隊赴地震災(zāi)區(qū)參與搶險工作．如圖，某探測隊在地面A、B兩處均探測出建筑物下方C處有生命跡象，已知探測線與地面的夾角分別是25°和60°，且AB=4米，求該生命跡象所在位置C的深度．（結(jié)果精確到1米．參考數(shù)據(jù)：sin25°≈0.4，cos25°≈0.9，tan25°≈0.5，≈1.7）3發(fā)布：2025/6/25 0:0:1組卷：2681引用：60難度：0.5 -
3．小劉同學(xué)在課外活動中觀察吊車的工作過程，繪制了如圖所示的平面圖形．已知吊車吊臂的支點(diǎn)O距離地面的高OO′=2米．當(dāng)?shù)醣垌敹擞葾點(diǎn)抬升至A′點(diǎn)（吊臂長度不變）時，地面B處的重物（大小忽略不計）被吊至B′處，緊繃著的吊纜A′B′=AB．AB垂直地面O′B于點(diǎn)B，A′B′垂直地面O′B于點(diǎn)C，吊臂長度OA′=OA=10米，且cosA=，sinA′=35．12
（1）求此重物在水平方向移動的距離BC；
（2）求此重物在豎直方向移動的距離B′C．（結(jié)果保留根號）發(fā)布：2025/6/25 0:30:1組卷：572引用：27難度：0.5
相關(guān)試卷