 【問題情境】:
【問題情境】:
我們知道若一個矩形的周長固定,當相鄰兩邊相等,即為正方形時,它的面積最大.反過來,若一個矩形的面積固定,它的周長是否會有最值呢?
【探究方法】:
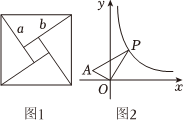
用兩個直角邊分別為a,b的4個全等的直角三角形可以拼成一個正方形.若a≠b,可以拼成如圖1所示的正方形,從而得到a2+b2>4×12ab,即a2+b2>2ab;當a=b時,中間小正方形收縮為1個點,此時正方形的面積等于4個直角三角形面積的和.即a2+b2=4(12ab)=2ab.于是我們可以得到結(jié)論:a,b為正數(shù),總有a2+b2≥2ab,當且僅當a=b時,代數(shù)式a2+b2取得最小值2ab.另外,我們也可以通過代數(shù)式運算得到類似上面的結(jié)論:
∵(a-b)2≥0,∴a2-2ab+b2≥0,a2+b2≥2ab;
∴對于任意實數(shù)a,b總有a2+b2≥2ab,且當a=b時,代數(shù)式a2+b2取最小值2ab.
使得上面的方法,對于正數(shù)a,b,試比較a+b和2ab的大小關(guān)系.
【類比應用】:
利用上面所得到的結(jié)論完成填空:
(1)當x>0時,代數(shù)式x+4x有最小值為 44.
(2)當x>1時,代數(shù)式x+6x-1有最值為 26+126+1.
(3)如圖2,已知P是反比例函數(shù)y=1x(x>0)圖象上任意一動點,O(0,0),A(-1,1),試求S△POA的最小面積.
a
2
+
b
2
>
4
×
1
2
ab
a
2
+
b
2
=
4
(
1
2
ab
)
=
2
ab
2
ab
x
+
4
x
x
+
6
x
-
1
2
6
+
1
2
6
+
1
y
=
1
x
(
x
>
0
)
【答案】4;
2
6
+
1
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:153引用:1難度:0.5
相似題
-
 1.如圖,在x軸上方有①~⑥六個臺階,它們的拐角T1~T6處均為90°,每個臺階的高、寬分別是1和2個單位長度,若反比例函數(shù)y=-的圖象經(jīng)過T1,則反比例函數(shù)y=12x的圖象經(jīng)過兩個工臺階的橫面(與x軸平行的面,包括橫面的兩端點),這兩個臺階是 和 .10x發(fā)布:2025/5/24 11:0:1組卷:115引用:3難度:0.5
1.如圖,在x軸上方有①~⑥六個臺階,它們的拐角T1~T6處均為90°,每個臺階的高、寬分別是1和2個單位長度,若反比例函數(shù)y=-的圖象經(jīng)過T1,則反比例函數(shù)y=12x的圖象經(jīng)過兩個工臺階的橫面(與x軸平行的面,包括橫面的兩端點),這兩個臺階是 和 .10x發(fā)布:2025/5/24 11:0:1組卷:115引用:3難度:0.5 -
2.長為300m的春游隊伍,以v(m/s)的速度向東行進,如圖1和圖2,當隊伍排尾行進到位置O時,在排尾處的甲有一物品要送到排頭,送到后立即返回排尾,甲的往返速度均為2v(m/s),當甲返回排尾后,他及隊伍均停止行進.設(shè)排尾從位置O開始行進的時間為t(s),排頭與O的距離為S頭(m).

(1)當v=2時,解答:
①求S頭與t的函數(shù)關(guān)系式(不寫t的取值范圍);
②當甲趕到排頭位置時,求S頭的值;在甲從排頭返回到排尾過程中,設(shè)甲與位置O的距離為S甲(m),求S甲與t的函數(shù)關(guān)系式(不寫t的取值范圍)
(2)設(shè)甲這次往返隊伍的總時間為T(s),求T與v的函數(shù)關(guān)系式(不寫v的取值范圍),并寫出隊伍在此過程中行進的路程.發(fā)布:2025/5/24 8:30:1組卷:3139引用:4難度:0.4 -
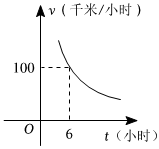 3.一輛客車從A地出發(fā)前往B地,平均速度v(千米/小時)與所用時間t(小時)的函數(shù)關(guān)系如圖所示,其中60≤v≤120.
3.一輛客車從A地出發(fā)前往B地,平均速度v(千米/小時)與所用時間t(小時)的函數(shù)關(guān)系如圖所示,其中60≤v≤120.
(1)求v與t的函數(shù)關(guān)系式及t的取值范圍;
(2)客車上午8點從A地出發(fā).客車需在當天14點至15點30分(含14點與15點30分)間到達B地,求客車行駛速度v的取值范圍.發(fā)布:2025/5/23 19:0:2組卷:355引用:1難度:0.6
相關(guān)試卷


