2023年山東省德州市夏津縣中考數學一模試卷

一、選擇題：每題4分，本大題共12小題，在每小題給出的四個選項中，只有一個是正確的，請把正確的選項選出來．每小題選對得4分，選錯、不選或選出的答案超過一個均記為零分．

• 1．在實數-2，-4.5，0，2中最小的實數是（　　）

  A．-2

  B．-4.5

  C．0

  D．2
  組卷：69引用：4難度：0.9

  解析

• 2．下列圖形中，是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：155引用：10難度：0.9

  解析

• 3．夏津縣地處魯西北平原，魯冀兩省交界處，因“齊晉會盟之要津”而得名，具有2200年歷史．據我縣統計局統計，2023年我縣常住人口為45.8萬，將45.8萬用科學記數法表示為（　　）

  A．45.8×104

  B．4.58×105

  C．4.58×106

  D．4.58×107
  組卷：11引用：2難度：0.9

  解析

• 4．如圖所示的幾何體，它的俯視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：13引用：2難度：0.8

  解析

• 5．下列運算正確的是（　　）

  A． 2 + 3 = 5

  B．（2a2）3=6a6

  C．2a2?3a=6a3

  D． （ - 3 ） 2 = - 3
  組卷：51引用：2難度：0.8

  解析

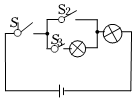• 6．如圖，電路連接完好，且各元件工作正常．隨機閉合開關S₁、S₂、S₃中的兩個，能讓兩個小燈泡同時發光的概率為（　　）

  A． 1 6

  B． 1 2

  C． 2 3

  D． 1 3
  組卷：360引用：9難度：0.5

  解析

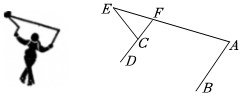• 7．某學校將國家非物質文化遺產——“抖空竹”引入陽光特色大課間，某同學“抖空竹”的一個瞬間如圖所示，若將左圖抽象成右圖的數學問題：在平面內，AB∥CD，DC的延長線交AE于點F；若∠BAE=75°，∠AEC=35°，則∠DCE的度數為（　　）

  A．120°

  B．115°

  C．110°

  D．75°
  組卷：321引用：9難度：0.8

  解析

• 8．如圖，用若干個全等的正五邊形排成圓環狀，圖中所示的是其中3個正五邊形的位置．要完成這一圓環排列，共需要正五邊形的個數是（　　）

  A．7個

  B．8個

  C．9個

  D．10個
  組卷：992引用：10難度：0.6

  解析

三、解答題：本大題共7小題，共記78分．解答要寫出必要的文字說明、證明過程或者演算步驟．

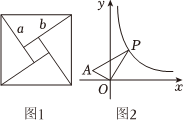• 24．【問題情境】：
  我們知道若一個矩形的周長固定，當相鄰兩邊相等，即為正方形時，它的面積最大．反過來，若一個矩形的面積固定，它的周長是否會有最值呢？
  【探究方法】：
  用兩個直角邊分別為a,b的4個全等的直角三角形可以拼成一個正方形．若a≠b,可以拼成如圖1所示的正方形，從而得到

  a

  2

  +

  b

  2

  ＞

  4

  ×

  1

  2

  ab

  ，即a²+b²＞2ab；當a=b時，中間小正方形收縮為1個點，此時正方形的面積等于4個直角三角形面積的和．即

  a

  2

  +

  b

  2

  =

  4

  （

  1

  2

  ab

  ）

  =

  2

  ab

  ．于是我們可以得到結論：a,b為正數，總有a²+b²≥2ab,當且僅當a=b時，代數式a²+b²取得最小值2ab.另外，我們也可以通過代數式運算得到類似上面的結論：
  ∵（a-b）²≥0，∴a²-2ab+b²≥0，a²+b²≥2ab；
  ∴對于任意實數a,b總有a²+b²≥2ab,且當a=b時，代數式a²+b²取最小值2ab.
  使得上面的方法，對于正數a,b,試比較a+b和

  2

  ab

  的大小關系．
  【類比應用】：
  利用上面所得到的結論完成填空：
  （1）當x＞0時，代數式

  x

  +

  4

  x

  有最小值為

  ．
  （2）當x＞1時，代數式

  x

  +

  6

  x

  -

  1

  有最值為

  ．
  （3）如圖2，已知P是反比例函數

  y

  =

  1

  x

  （

  x

  ＞

  0

  ）

  圖象上任意一動點，O（0，0），A（-1，1），試求S_△POA的最小面積．
  組卷：153引用：1難度：0.5

  解析

• 25．已知點P是二次函數

  y

  1

  =

  -

  （

  x

  -

  m

  +

  1

  ）

  2

  +

  m

  2

  -

  m

  -

  1

  圖象的頂點．
  
  （1）小明發現，對m取不同的值時，點P的位置也不同，但是這些點都在某一個函數的圖象上，請協助小明完成對這個函數表達式的探究：
  ①將下表填寫完整：
  

  m	-1	0	1	2	3
  P點坐標	（-2，1）	（-1，-1）

  ②描出表格中的五個點，猜想這些點在哪個函數的圖象上？求出這個圖象對應的函數表達式，并加以驗證；
  （2）若過點（0，2），且平行于x軸的直線與

  y

  1

  =

  -

  （

  x

  -

  m

  +

  1

  ）

  2

  +

  m

  2

  -

  m

  -

  1

  的圖象有兩個交點A和B，與②中得到的函數圖象有兩個交點C和D，當AB=CD時，請求出此時的m值，寫出求解過程；
  （3）若

  E

  （

  -

  1

  ，-

  5

  4

  ）

  ，

  F

  （

  3

  ，-

  5

  4

  ）

  ，函數

  y

  1

  =

  -

  （

  x

  -

  m

  +

  1

  ）

  2

  +

  m

  2

  -

  m

  -

  1

  的圖象與線段EF只有一個公共點，請結合函數圖象，直接寫出m的取值范圍．
  組卷：117引用：3難度：0.2

  解析