課題學習：平行線的“等角轉化”功能．
| 如圖1，已知點A是BC外一點，連接AB，AC．求∠BAC+∠B+∠C的度數． 解：過點A作ED∥BC， ∴∠B= ∠EAB ∠EAB ，∠C=∠DAC ∠DAC ．又∵∠EAB+∠BAC+∠DAC=180°． ∴∠B+∠BAC+∠C=180°． |
（1）閱讀并補充推理過程．
解題反思：
從上面的推理過程中，我們發(fā)現平行線具有“等角轉化”的功能，將∠BAC，∠B，∠C“湊”在一起，得出角之間的關系，使問題得以解決．
方法運用：
（2）如圖2，已知AB∥CD，∠BEC=80°，求∠B-∠C的度數．（提示：過點E作AB或CD的平行線．）
深化拓展：
（3）如圖3，如圖，AB∥CD，BF，CG分別平分∠DCE，∠ABE，且所在直線交于點F，∠E=80°，則∠F=
50°
50°
．
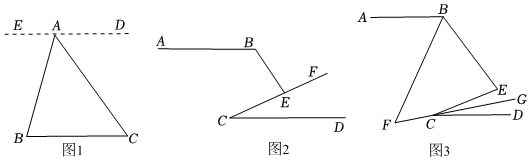
【答案】∠EAB；∠DAC；50°
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：204引用：5難度：0.6
相似題
-
1．如圖，已知在△ABC中，∠A=90°．
（1）請用圓規(guī)和直尺作出⊙P，使圓心P在AC邊上，且與AB，BC兩邊都相切（保留作圖痕跡，不寫作法和證明）；
（2）若AB=4，AC=3，試求（1）中⊙P的半徑；發(fā)布：2025/5/23 21:30:2組卷：29引用：2難度：0.5 -
2．如圖，在△ABC中，∠BAC=90°，∠C=30°，請你用無刻度的直尺和圓規(guī)作⊙P，使得⊙P與AB相切于點A，同時與BC相切．（保留作圖痕跡，不寫作法）發(fā)布：2025/5/23 22:30:2組卷：29引用：1難度：0.4 -
3．如圖，BD是△ABC的角平分線，請用尺規(guī)作圖法求作△ABC的內心．（保留作圖痕跡，不寫作法）發(fā)布：2025/5/23 22:0:2組卷：38引用：5難度：0.7