點P是平面直角坐標系中的一點且不在坐標軸上，過點P向x軸，y軸作垂線段，若垂線段的長度的和為4，則點P叫做“垂距點”．例如：如圖中的P（1，3）是“垂距點”．
（1）在點A（2，2），B（32，-52），C（-1，5）中，是“垂距點”的點為 A，BA，B；
（2）求函數y=2x+3的圖象上的“垂距點”的坐標．
（3）⊙T的圓心T的坐標為（1，0），半徑為r.若⊙T上存在“垂距點”，則r的取值范圍是 322≤r＜5322≤r＜5．
A
（
2
，
2
）
，
B
（
3
2
，-
5
2
）
，
C
（
-
1
，
5
）
3
2
2
≤
r
＜
5
3
2
2
≤
r
＜
5
【考點】圓的綜合題．
【答案】A，B；
3
2
2
≤
r
＜
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：136引用：3難度：0.4
相似題
-
1．等腰三角形AFG中AF=AG，且內接于圓O，D、E為邊FG上兩點（D在F、E之間），分別延長AD、AE交圓O于B、C兩點（如圖1），記∠BAF=α，∠AFG=β．
（1）求∠ACB的大小（用α，β表示）；
（2）連接CF，交AB于H（如圖2）．若β=45°，且BC×EF=AE×CF．求證：∠AHC=2∠BAC；
（3）在（2）的條件下，取CH中點M，連接OM、GM（如圖3），若∠OGM=2α-45°，
①求證：GM∥BC，GM=BC；12
②請直接寫出的值．OMMC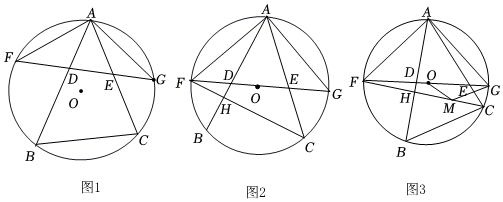
發布：2025/6/7 16:0:2組卷：1490引用：8難度：0.1 -
2．已知，線段AB是⊙O的直徑，弦CD⊥AB于點H，點M是優弧CBD上的任意一點，AH=2，CH=4．
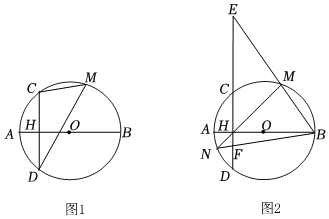
（1）如圖1，
①求⊙O的半徑；
②求sin∠CMD的值．
（2）如圖2，直線BM交直線CD于點E，直線MH交⊙O于點N，連結BN交CD于點F，求HE?FH的值．發布：2025/6/7 7:0:1組卷：476引用：2難度：0.3 -
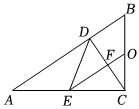3．如圖，在Rt△ABC中，∠ACB=90°，過點C作CD⊥AB于點D，O為BC的中點，E是AC的中點，連接OE交CD于點F．
（1）若∠BCD=30°，BC=20，求BD的長；
（2）若∠BCD=30°，求證：以BC為直徑的圓與DE相切；
（3）求證：2CE2=AB?EF．發布：2025/6/8 19:30:1組卷：18引用：1難度：0.4