綜合與實踐．
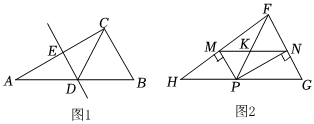
課間，小鑫在草稿紙上畫了一個直角三角形．如圖1，在Rt△ABC中，∠ACB=90°，他想到了作AC的垂直平分線ED，交AC于點E，交AB于點D．他和同桌開始探討線段AD與BD的大小關系．
（1）嘗試探究：當∠A=30°時，直接寫出線段AD與BD的大小關系：AD ==BD．（填“＞”、“＜”或“=”）
（2）得出結論：若∠A為任意銳角，則線段AD與BD的大小關系是AD ==BD，請說明理由．（填“＞”、“＜”或“=”）
（3）應用結論：利用上面的結論繼續研究，如圖2，P是△FHG的邊HG上的一個動點，PM⊥FH于點M，PN⊥FG于點N，FP與MN交于點K．當點P運動到某處時，MN與FP正好互相垂直，此時FP平分∠HFG嗎？請說明理由．
【考點】三角形綜合題．
【答案】=；=
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：36引用：2難度：0.1
相似題
-
1．在平面直角坐標系中，點A在x軸正半軸上，點B在y軸正半軸上，∠ABC=90°，且AB=BC．
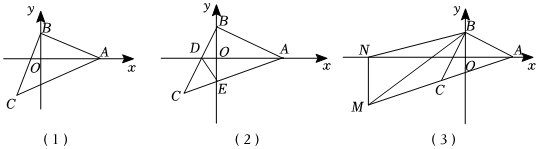
（1）如圖（1），A（5，0），B（0，2），點C在第三象限，請直接寫出點C的坐標；
（2）如圖（2），BC與x軸交于點D，AC與y軸交于點E，若點D為BC的中點，求證：∠ADB=∠CDE；
（3）如圖（3），A（a,0），M在AC延長線上，過點M（m,-a）作MN⊥x軸于N，探究線段BM，AN，OB之間的數量關系，并證明你的結論．發布：2025/5/31 4:30:2組卷：490引用：2難度：0.4 -
2．在平面直角坐標系xOy中，對于點P，點M給出如下定義：如果點P與原點O的距離為a,點M與點P的距離是a的k倍（k為整數），那么稱點M為點P的“k倍關聯點”．
（1）當P1（-1.5，0）時．
①如果點P1的2倍關聯點M在x軸上，那么點M的坐標為 ；
②如果點M（x,y）是點P1的k倍關聯點，且滿足x=-1.5，-3≤y≤5，那么整數k的最大值為 ；
（2）已知在Rt△ABC中，∠ABC=90°，∠ACB=30°，A（b,0），B（b+1，0）．若P2（-1，0），且在△ABC的邊上存在點P2的2倍關聯點Q，求b的取值范圍．發布：2025/5/31 7:30:1組卷：750引用：2難度：0.3 -
3．問題提出
如圖（1），△ABC和△DEC都是等腰直角三角形，其中∠ACB=∠DCE=90°，BC=AC，EC=DC，點E在△ABC內部，直線AD與BE交于點F．線段AF，BF，CF之間存在怎樣的數量關系？
問題探究
（1）先將問題特殊化如圖2，當點D，F重合時，直接寫出表示AF，BF，CF之間的數量關系的等式：；
（2）再探究一般情形如圖1，當點D，F不重合時，證明（1）中的結論仍然成立．（提示：過點C作CG⊥CF，交BF于點G）
問題拓展
如圖3，若△ABC和△DEC都是含30°的直角三角形，有∠ACB=∠DCE=90°，∠BAC=∠EDC=30°，點E在△ABC內部，直線AD與BE交于點F．直接寫出一個等式，表示線段AF，BF，CF之間的數量關系．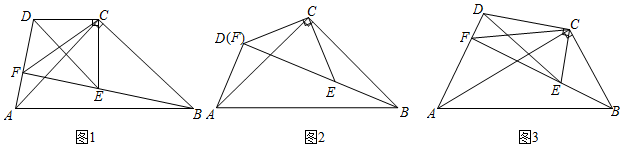
發布：2025/5/31 6:0:2組卷：1797引用：8難度：0.1