小慧在課外閱讀時遇到了一個與勾股定理有關的故事：古希臘哲學家柏拉圖對勾股定理很有研究，曾得到勾股數的一個結論：如果m表示大于1的整數，則a=2m,b=m2-1，c=m2+1構成勾股數，你能證明柏拉圖這個結論嗎？并利用這個結論寫出兩組勾股數．（勾股數定義：若三角形三邊長a、b、c都是正整數，且滿足a2+b2=c2，那么a、b、c稱為一組勾股數）．
【答案】證明過程見解答；8，15，17；5，12，13．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/25 1:0:1組卷：29引用：1難度：0.5
相似題
-
1．如圖是“趙爽弦圖”，△ABH、△BCG、△CDF和△DAE是四個全等的直角三角形，四邊形ABCD和EFGH都是正方形．如果AB=10，EF=2，那么AH等于．發布：2025/6/23 0:0:1組卷：9104引用：71難度：0.7 -
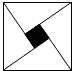2．如圖，是由四個直角邊分別為3和4全等的直角三角形拼成的“趙爽弦圖”，那么陰影部分面積為．發布：2025/6/24 12:30:2組卷：896引用：13難度：0.9 -
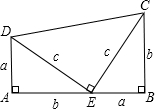3．歷史上對勾股定理的一種證法采用了下列圖形：其中兩個全等的直角三角形邊AE、EB在一條直線上．證明中用到的面積相等關系是（ ）發布：2025/6/21 17:0:2組卷：1052引用：15難度：0.7