根據(jù)以下素材,探索完成任務(wù).
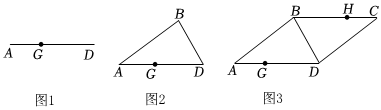
| 素材1 | 定義:如圖1,點(diǎn)G將線段AD分成兩部分,如果 AG GD = GD AD |
| 素材2 | 某興趣小組在進(jìn)行研究性學(xué)習(xí)時(shí),由黃金分割點(diǎn)聯(lián)想到“黃金分割線”,類似地給出黃金分割線的定義:直線l將一個(gè)面積為S的圖形分成面積分別為S1,S2的兩部分,如果 S 1 S 2 = S 2 S |
| 素材3 | 平行四邊形是中心對(duì)稱圖形:在同一平面內(nèi),一個(gè)三角形繞其中一邊的中點(diǎn)旋轉(zhuǎn)180°,其余兩邊與旋轉(zhuǎn)后相對(duì)應(yīng)的兩邊組成一個(gè)平行四邊形,例如,圖2中的△ABD繞BD的中點(diǎn)旋轉(zhuǎn)180°后與原三角形組成一個(gè)平行四邊形ABCD(如圖3). |
|
|
| 問(wèn)題解決 | |
| 任務(wù)1 | 問(wèn)題1:如圖3,AD邊上黃金分割點(diǎn)G旋轉(zhuǎn)后的對(duì)稱點(diǎn)H是否也是BC邊上的黃金分割點(diǎn)?請(qǐng)寫出你的判斷結(jié)論,并說(shuō)明理由. 問(wèn)題2:直線GH是不是四邊形ABCD的黃金分割線?請(qǐng)寫出你的判斷結(jié)論: 直線GH不是四邊形ABCD的黃金分割線 直線GH不是四邊形ABCD的黃金分割線 . |
| 任務(wù)2 | 請(qǐng)?jiān)趫D3探索:BC邊上是否存在點(diǎn)M,使得直線GM是四邊形ABCD的黃金分割線?如果存在,請(qǐng)說(shuō)明點(diǎn)M的位置;如果不存在,請(qǐng)說(shuō)明理由. |
| 任務(wù)3 | 興趣小組探索圖2時(shí)猜想:在△ABD中,若點(diǎn)G為AD邊上的黃金分割點(diǎn),連接BG,則直線BG是△ABD的黃金分割線,你認(rèn)為對(duì)嗎?為什么? |
| 任務(wù)4 | 興趣小組探索圖2時(shí)還發(fā)現(xiàn):若點(diǎn)G是△ABD的邊AD的黃金分割點(diǎn),過(guò)點(diǎn)B任意作一條直線交GD于點(diǎn)E,再過(guò)點(diǎn)G作GF∥BE交AB于點(diǎn)F,則直線EF是△ABD的黃金分割線,請(qǐng)你給出證明. |
【答案】直線GH不是四邊形ABCD的黃金分割線
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2025/6/4 3:30:2組卷:456引用:4難度:0.4
相似題
-
1.若點(diǎn)C是線段AB的黃金分割點(diǎn),AB=8cm,AC>BC,則AC等于 cm.
發(fā)布:2025/6/4 13:0:1組卷:262引用:3難度:0.7 -
2.二次根式的除法,要化去分母中的根號(hào),需將分子、分母同乘以一個(gè)恰當(dāng)?shù)亩胃剑?br />例如:化簡(jiǎn):
.12-1
解:將分子、分寫同乘以得2+1=12-1=2+1(2-1)(2+1).2+1
類比應(yīng)用:(1)化簡(jiǎn):=.123-11
(2)化簡(jiǎn):+12+1+…+13+2.19+8
拓展延伸:寬與長(zhǎng)的比是的矩形叫黃金矩形,如圖①,已知黃金矩形ABCD的寬AB=1.5-12
(1)黃金矩形ABCD的長(zhǎng)BC=;
(2)如圖②,將圖①中的黃金矩形裁剪掉一個(gè)以AB為邊的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否為黃金矩形,并證明你的結(jié)論;
(3)在圖②中,連接AE,則點(diǎn)D到線段AE的距離為.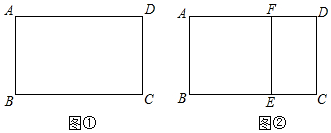 發(fā)布:2025/6/5 3:0:1組卷:1225引用:3難度:0.5
發(fā)布:2025/6/5 3:0:1組卷:1225引用:3難度:0.5 -
 3.如果我們身旁沒(méi)有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法:
3.如果我們身旁沒(méi)有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法:
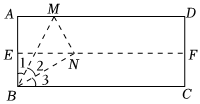
第一:對(duì)折矩形紙片ABCD,使AD與BC重合,得到折痕EF,把紙片展平.
第二:再一次折疊紙片,使點(diǎn)A落在EF上,并使折痕經(jīng)過(guò)點(diǎn)B,得到折痕BM和線段BN.
(1)請(qǐng)問(wèn)圖中∠1、∠2和∠3有什么關(guān)系?證明你的結(jié)論.
(2)在第(1)題圖中,延長(zhǎng)BN交AD于G,過(guò)G點(diǎn)作GH⊥BC于點(diǎn)H,得出一個(gè)以DG為寬的黃金矩形GHCD(黃金矩形就是符合黃金比例的矩形,即寬與長(zhǎng)的比值為),若已知AB=4,求BC的長(zhǎng).5-12發(fā)布:2025/6/5 20:0:2組卷:214引用:2難度:0.4


