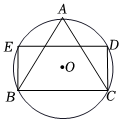
如圖，⊙O的半徑為2，△ABC是⊙O的內接等邊三角形，點DE在⊙O上．四邊形BCDE為平行四邊形，則平行四邊形BCDE的面積是（ ）
【答案】A
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：127引用：2難度：0.5
相似題
-
1．如圖，在等腰直角△ACB中，∠ACB=90°，BC=5，點E是AB邊上一點（點E不與點
A，B重合），連接CE，線段CE繞點C順時針旋轉90°得到線段CD，連接AD，DE，線段DE與AC邊交于點F，有以下說法：
Ⅰ．四邊形AECD的面積總等于；252
Ⅱ．當時，△AED的外接圓半徑為BE=2．342
下列判斷正確的是（ ）發布：2025/5/22 16:30:1組卷：110引用：3難度：0.4 -
2．如圖，⊙O是△ABC的外接圓，AD是⊙O的直徑，若∠CAD=75°，則∠B的度數是 ．發布：2025/5/22 17:0:1組卷：234引用：10難度：0.6 -
3．請閱讀下列材料，并完成相應的任務：
阿基米德折弦定理
阿基米德（archimedes,公元前287～公元前212年，古希臘）是有史以來最偉大的數學家之一，他與牛頓、高斯并稱為三大數學王子．
阿拉伯Al-Birnmi（973～1050年）的譯文中保存了阿基米德折弦定理的內容，蘇聯在1964年根據Al-Birnmi譯本出版了俄文版《阿基米德全集》，第一題就是阿基米德折弦定理．
阿基米德折弦定理：如圖1，AB和BC是⊙O的兩條弦（即折線ABC是圓的一條折弦），AB＞BC，D是的中點，則從D向AB所作垂線的垂足E是折弦ABC的中點，即AE=EB+BC．?ABC
下面是運用“補短法”證明AE=EB+BC的部分證明過程．
證明：如圖2，延長CB到點F，使得CF=AE，連接DA、DB、DC和DF．
∵D是的中點，?ABC
∴DA=DC．
任務：
（1）請按照上面的證明思路，寫出該證明的剩余部分；
（2）已知等邊△ABC內接于⊙O，AB=6，D為⊙O上一點，∠ABD=45°，AE⊥BD于點E，求△BDC的周長是 ．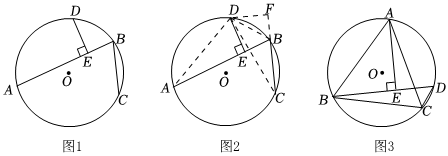
發布：2025/5/22 15:30:1組卷：579引用：1難度：0.3