如圖，在平面直角坐標(biāo)系xOy中，已知拋物線L：y=-x2+bx+c與x軸交于A（-3，0），與y軸交于點C（0，3）．
（1）求拋物線L的表達(dá)式和頂點坐標(biāo)D；
（2）將拋物線L平移得到L′，拋物線L′的頂點坐標(biāo)為E，L′的對稱軸與x軸交于點F．若以O(shè)，E，F(xiàn)為頂點的三角形與△AOC全等，請你寫出平移過程，并說明理由．
【考點】二次函數(shù)綜合題．
【答案】（1）拋物線L：y=-x2-2x+3，頂點D（-1，4）；
（2）拋物線L向右平移4個單位，向下平移1個單位或向右平移4個單位，向下平移7個單位或向左平移2個單位，向下平移1個單位或向左平移2個單位，向下平移7個單位得到拋物線L′．
（2）拋物線L向右平移4個單位，向下平移1個單位或向右平移4個單位，向下平移7個單位或向左平移2個單位，向下平移1個單位或向左平移2個單位，向下平移7個單位得到拋物線L′．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/5/7 8:0:9組卷：305引用：1難度：0.2
相似題
-
1．已知拋物線y=ax2+bx+3 經(jīng)過點A（2，3）．
（1）用含a的式子表示b；
（2）若拋物線開口向上，點P（m,n）是拋物線上一動點，當(dāng)-1≤m≤2時，n的最大值是5，求a的值．
（3）將點M（-1，4）向右平移5個單位長度得到點N，若線段MN與拋物線只有一個公共點，直接寫出a的取值范圍．發(fā)布：2025/5/22 20:30:1組卷：459引用：1難度：0.3 -
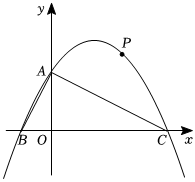2．已知，如圖，在平面直角坐標(biāo)系中，Rt△ABC的斜邊BC在x軸上，直角頂點A在y軸的正半軸上，AB=，AC=25．5
（1）求A、B、C三點的坐標(biāo)；
（2）求過A、B、C三點的拋物線的解析式和對稱軸；
（3）設(shè)點P是拋物線在第一象限部分上的點，△PAC的面積為S，求使S面積最大時點P的坐標(biāo)；
（4）在拋物線對稱軸上，是否存在這樣點M，使得△AMP為等腰三角形？若存在，請直接寫出點M的坐標(biāo)；若不存在，請說明理由．發(fā)布：2025/5/22 20:30:1組卷：67引用：1難度：0.4 -
3．對于某些三角形，我們可以直接用面積公式或是用割補(bǔ)法等來求它們的面積，下面我們研究一種求面積的新方法：如圖1所示，分別過三角形的頂點A、C作水平線的鉛垂線l1、l2，l1、l2之間的距離d叫做水平寬；如圖1所示，過點B作水平線的鉛垂線交AC于點D，稱線段BD的長叫做這個三角形的鉛垂高．
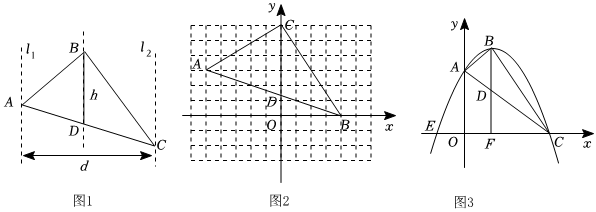
結(jié)論提煉：容易證明，“三角形的面積等于水平寬與鉛垂高乘積的一半”，即“”．S=12dh
嘗試應(yīng)用：
已知：如圖2，點A（-5，3）、B（4，0）、C（0，6），則△ABC的水平寬為 ，鉛垂高為 ，所以△ABC的面積為 ．
學(xué)以致用：
如圖3，在平面直角坐標(biāo)系中，拋物線的解析式為：y=-x2+2x+3，點B為拋物線的頂點，圖象與y軸交于點A，與x軸交于E、C兩點，BD為△ABC的鉛垂高，延長BD交x軸于點F，則頂點B坐標(biāo)為 ，鉛垂高BD=，△ABC的面積為 ．發(fā)布：2025/5/22 20:30:1組卷：579引用：1難度：0.4
相關(guān)試卷