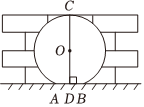
如圖是某風景區的一個圓拱形門（示意圖），凈高CD為5米，路面AB的寬為2米，求圓拱形門所在⊙O的半徑．
【考點】垂徑定理的應用．
【答案】2.6米．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/7 8:0:9組卷：29引用：1難度：0.5
相似題
-
1．在古代，智慧的勞動人民已經會使用“石磨”，其原理為在磨盤的邊緣連接一個固定長度的“杠桿”，推動“杠桿”帶動磨盤轉動，將糧食磨碎．如圖，AB為圓O的直徑，AC是⊙O的一條弦，D為弧BC的中點，作DE⊥AC交AC的延長線于點E，交AB的延長線于點F，連接DA．
（1）若AB=90cm,則圓心O到“杠桿EF”的距離是多少？說明你的理由；
（2）若，求陰影部分的面積．（結果保留π）DA=DF=63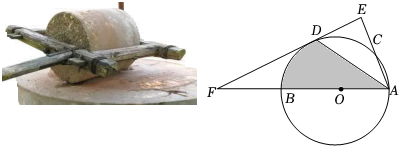
發布：2025/5/26 1:30:1組卷：1130引用：11難度：0.6 -
2．在直徑為10m的圓柱形油槽內注入一些油后，截面如圖所示，液面寬AB=6m,如果繼續向油槽內注油，使液面寬為8m,那么液面上升了（ ）m.發布：2025/5/26 4:0:1組卷：500引用：5難度：0.6 -
3．請閱讀下列材料，并完成相應的任務：
阿基米德折弦定理，阿基米德（公元前287年一公元前212年），偉大的古希臘哲學家、百科式科學家、數學家、物理學家、力學家，靜態力學和流體靜力學的奠基人，并且享有“力學之父”的美稱，阿基米德和高斯，牛頓并列為世界三大數學家．
阿拉伯Al-Binmi（973年一1050年）的譯文中保存了阿基米德折弦定理的內容，蘇聯在1964年根據Al-Binmi譯本出版了俄文版《阿基米德全集》，第一題就是阿基米德折弦定理．
阿基米德折弦定理：如圖1，AB和BC是⊙O的兩條弦（即折線ABC是圓的一條折弦），BC＞AB，M是的中點，則從M向BC所作垂線的垂足D是折弦ABC的中點，即CD=AB+BD．?ABC
小明同學運用“截長法”和三角形全等來證明CD=AB+BD，過程如下：
證明：如圖2所示，在CB上截取CG=AB，連接MA，MB，MC和MG．
∵M是的中點，∴MA=MC，…?ABC
任務：
（1）請按照上述思路，寫出該證明的剩余部分；
（2）如圖3，已知等邊△ABC內接于⊙O，AB=4，D為上一點，∠ABD=45°，AE⊥BD于點E，請直接寫出△BDC的周長．?AC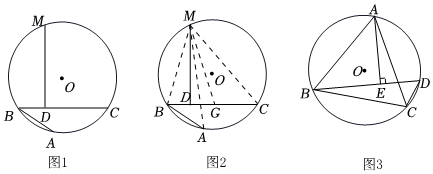
發布：2025/5/26 6:30:2組卷：234引用：1難度：0.4