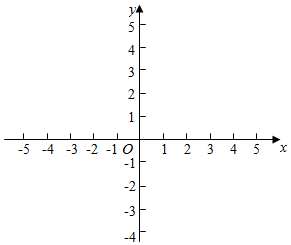對(duì)于平面直角坐標(biāo)系xOy中的任意一點(diǎn)P，給出如下定義：經(jīng)過點(diǎn)P且平行于兩坐標(biāo)軸夾角平分線的直線，叫做點(diǎn)P的“特征線”．
例如：點(diǎn)M（1，3）的特征線是y=x+2和y=-x+4；
（1）若點(diǎn)D的其中一條特征線是y=x+1，則在D1（2，2）、D2（-1，0）、D3（-3，4）三個(gè)點(diǎn)中，可能是點(diǎn)D的點(diǎn)有D2D2；
（2）已知點(diǎn)P（-1，2）的平行于第二、四象限夾角平分線的特征線與x軸相交于點(diǎn)A，直線y=kx+b（k≠0）經(jīng)過點(diǎn)P，且與x軸交于點(diǎn)B．若使△BPA的面積不小于6，求k的取值范圍；
（3）已知點(diǎn)C（2，0），T（t,0），且⊙T的半徑為1．當(dāng)⊙T與點(diǎn)C的特征線存在交點(diǎn)時(shí)，直接寫出t的取值范圍．
【考點(diǎn)】圓的綜合題．
【答案】D2
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/12 12:0:9組卷：359引用：3難度：0.1
相似題
-
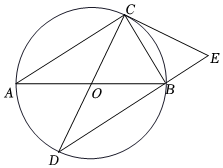1．如圖，△ABC內(nèi)接于⊙O，AB，CD是⊙O的直徑，E是DB延長(zhǎng)線上一點(diǎn)，且∠DEC=∠ABC．
（1）求證：CE是⊙O的切線；
（2）若DE=4，AC=2BC，求線段CE的長(zhǎng)．5發(fā)布：2025/5/24 9:0:1組卷：1754引用：15難度：0.3 -
2．如圖1，菱形ABCD的邊長(zhǎng)為12cm,∠B=60°，M，N分別在邊AB，CD．上，AM=3cm,DN=4cm,點(diǎn)P從點(diǎn)M出發(fā)，沿折線MB-BC以1cm/s的速度向點(diǎn)C勻速運(yùn)動(dòng)（不與點(diǎn)C重合）；△APC的外接圓⊙O與CD相交于點(diǎn)E，連接PE交AC于點(diǎn)F．設(shè)點(diǎn)P的運(yùn)動(dòng)時(shí)間為t s.
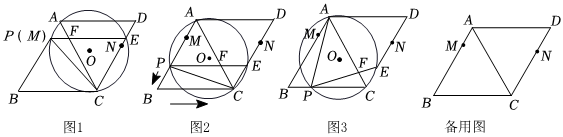
（1）∠APE=°；
（2）若⊙O與AD相切，
①判斷⊙O與CD的位置關(guān)系；
②求的長(zhǎng)；?APC
（3）如圖3，當(dāng)點(diǎn)P在BC上運(yùn)動(dòng)時(shí)，求CF的最大值，并判斷此時(shí)PE與AC的位置關(guān)系；
（4）若點(diǎn)N在⊙O的內(nèi)部，直接寫出t的取值范圍．發(fā)布：2025/5/24 9:0:1組卷：178引用：3難度：0.1 -
3．如圖，AB是⊙O的直徑，點(diǎn)D是
上的一點(diǎn)，且∠BDE=∠CBE，BD與AE交于F點(diǎn)．?AE
（1）求證BC是圓O的切線；
（2）若BD平分∠ABE，求證：DE2=DF?DB；
（3）在（2）的條件下，延長(zhǎng)ED、BA交于點(diǎn)P，若PA=AO，DE=2，求⊙O的半徑．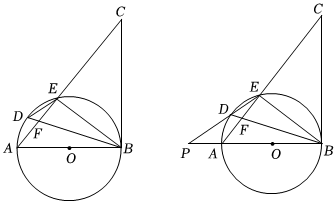
發(fā)布：2025/5/24 9:0:1組卷：178引用：2難度：0.3