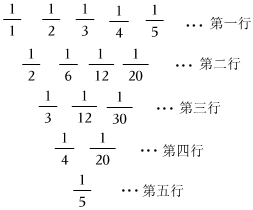
如圖，有這么一個數陣，將
1
1
，
1
2
，
1
3
，
1
4
，…，
1
n
，…作為第一行，相鄰兩個數相減作為第二行，以此類推．則第3行前8個數之和為（　　）

A．

B．

C．

D．

【答案】B

【解答】

【點評】

聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。

發(fā)布：2025/5/30 12:30:2組卷：84引用：1難度：0.6

相似題

1．觀察下列等式：
1
1
×
2
=
1
-
1
2
，
1
2
×
3
=
1
2
-
1
3
，
1
3
×
4
=
1
3
-
1
4
…
（1）仿照上面的等式，把后面這個代數式寫成上面等式右邊的形式：
1
n
（
n
+
1
）
=
；
（2）直接寫出下面算式的結果：
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+
…
+
1
2019
×
2020
=
；
以下兩小題，需寫出解答過程：
（3）計算：
|
1
2
-
1
|
+
|
1
3
-
1
2
|
+
…
+
|
1
99
-
1
98
|
+
|
1
100
-
1
99
|
；
（4）探究并計算：
1
2
×
4
+
1
4
×
6
+
1
6
×
8
+
…
+
1
2006
×
2008
．
發(fā)布：2025/5/31 13:30:2組卷：239引用：1難度：0.6
解析
2．有一列數：a₁，a₂，a₃，a₄，…，a_n-1，a_n，其中a₁=5×2+1，a₂=5×3+2，a₃=5×4+3，a₄=5×5+4，a₅=5×6+5，…，當a_n=2021時，n的值為
．
發(fā)布：2025/5/31 17:0:8組卷：281引用：4難度：0.5
解析
3．觀察下列等式：
第1個等式：
2
1
-
5
3
=
1
3
，
第2個等式：
2
2
-
6
8
=
1
4
，
第3個等式：
2
3
-
7
15
=
1
5
，
…
按照以上規(guī)律，解決下列問題：
（1）寫出第4個等式：
；
（2）寫出你猜想的第n個等式：
，并給出證明．
發(fā)布：2025/5/31 14:0:2組卷：88引用：2難度：0.7
解析

相關試卷

如圖，有這么一個數陣，將11，12，13，14，…，1n，…作為第一行，相鄰兩個數相減作為第二行，以此類推．則第3行前8個數之和為（ ）