觀察下列等式：
第1個等式：21-53=13，
第2個等式：22-68=14，
第3個等式：23-715=15，
…
按照以上規(guī)律，解決下列問題：
（1）寫出第4個等式：24-824=1624-824=16；
（2）寫出你猜想的第n個等式：2n-n+4（n+1）2-1=1n+22n-n+4（n+1）2-1=1n+2，并給出證明．
2
1
-
5
3
=
1
3
2
2
-
6
8
=
1
4
2
3
-
7
15
=
1
5
2
4
8
24
1
6
2
4
8
24
1
6
2
n
n
+
4
（
n
+
1
）
2
-
1
1
n
+
2
2
n
n
+
4
（
n
+
1
）
2
-
1
1
n
+
2
【考點(diǎn)】規(guī)律型：數(shù)字的變化類．
【答案】-=；-=
2
4
8
24
1
6
2
n
n
+
4
（
n
+
1
）
2
-
1
1
n
+
2
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/31 14:0:2組卷：88引用：2難度：0.7
相似題
-
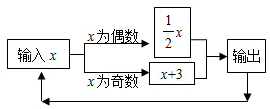1．如圖所示的運(yùn)算程序中，若開始輸入的x值為24，我們發(fā)現(xiàn)第1次輸出的結(jié)果為12，第2次輸出的結(jié)果為6，…，則第2021次輸出的結(jié)果為 ．發(fā)布：2025/6/1 23:30:1組卷：77引用：3難度：0.7 -
2．正整數(shù)按如圖所示的規(guī)律排列，則第9行、第10列的數(shù)字是（ ）
發(fā)布：2025/6/2 2:0:16組卷：270引用：1難度：0.6 -
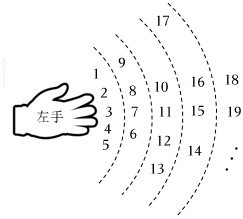3．如圖，按大拇指、食指、中指、無名指、小指、無名指、中指…的順序從1開始數(shù)數(shù)，當(dāng)數(shù)到2022時，對應(yīng)的手指是（ ）發(fā)布：2025/6/2 0:30:1組卷：127引用：2難度：0.7