已知△ABC≌△DEC，AB=AC，AB＞BC．現(xiàn)將△ABC和△DEC按如圖（1）、圖（2）的方式擺放，連接BD．
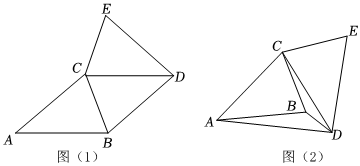
（1）如圖（1）．
①若∠A=40°，請直接寫出∠E的度數(shù)；
②若CB平分∠ACD，求證：DB=DC．
（2）如圖（2），連接AD，若∠BAD=∠BCD，試在線段AD上確定一點(diǎn)M，連接BM，使得△BAM≌△DCB，求∠BMD的度數(shù)．
【考點(diǎn)】三角形綜合題．
【答案】（1）①∠E=70°；
②證明過程見解答；
（2）∠BMD的度數(shù)為30°．
②證明過程見解答；
（2）∠BMD的度數(shù)為30°．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/29 19:0:1組卷：171引用：1難度：0.1
相似題
-
1．閱讀理解，自主探究：
“一線三垂直”模型是“一線三等角”模型的特殊情況，即三個(gè)等角角度為90°，于是有三組邊相互垂直．所以稱為“一線三垂直模型”．當(dāng)模型中有一組對(duì)應(yīng)邊長相等時(shí)，則模型中必定存在全等三角形．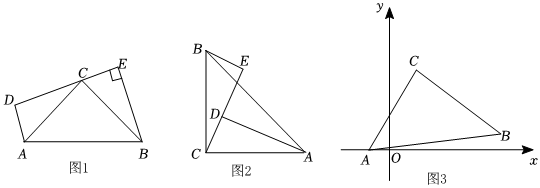
（1）問題解決：如圖1，在等腰直角△ABC中，∠ACB=90°，AC=BC，過點(diǎn)C作直線DE，AD⊥DE于D，BE⊥DE于E，則CD與BE的數(shù)量關(guān)系是 ；
（2）問題探究：如圖2，在等腰直角△ABC中，∠ACB=90°，AC=BC，過點(diǎn)C作直線CE，AD⊥CE于D，BE⊥CE于E，AD=2.5cm,DE=1.6cm,求BE的長；
（3）拓展延伸：如圖3，在平面直角坐標(biāo)系中，A（-1.5，0），C（1.5，3.5），△ABC為等腰直角三角形，∠ACB=90°，AC=BC，求B點(diǎn)坐標(biāo)．發(fā)布：2025/6/3 6:0:2組卷：1023引用：4難度：0.1 -
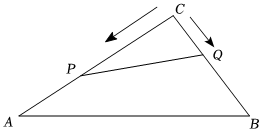2．在Rt△ABC中，∠C=90°，AC=20cm,BC=15cm.現(xiàn)有動(dòng)點(diǎn)P從點(diǎn)A出發(fā)，沿AC向點(diǎn)C方向運(yùn)動(dòng)，動(dòng)點(diǎn)Q從點(diǎn)C出發(fā)，沿線段CB也向點(diǎn)B方向運(yùn)動(dòng)．如果點(diǎn)P的速度是4cm/秒，點(diǎn)Q的速度是2cm/秒，它們同時(shí)出發(fā)，當(dāng)有一點(diǎn)到達(dá)所在線段的端點(diǎn)時(shí)，就停止運(yùn)動(dòng)．設(shè)運(yùn)動(dòng)的時(shí)間為t秒．
（1）用含t的代數(shù)式表示Rt△CPQ的面積S；
（2）當(dāng)t=3秒時(shí)，這時(shí)P、Q兩點(diǎn)之間的距離是多少？
（3）是否存在時(shí)刻t,使△CPQ的面積是△ABC的面積的？若有請求出；若沒有，請說明理由．23發(fā)布：2025/6/3 9:0:1組卷：36引用：1難度：0.2 -
3．關(guān)于等邊三角形，有很多值得我們探究的，在一次數(shù)學(xué)課上，老師出示了如下框中的題目．
第一小組討論后，進(jìn)行了如下解答：已知：如圖，在等邊△ABC中，點(diǎn)D在AC上，點(diǎn)E在BC的延長線，且BD=ED．試判斷AD與CE的數(shù)量關(guān)系，并說明理由．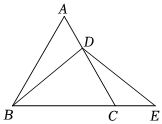 
（1）特殊情況，探索結(jié)論
當(dāng)點(diǎn)D為AC的中點(diǎn)時(shí)，如圖1，線段AD CE．（填“＞”，“＜”或“=”）
（2）特例啟發(fā)，解答題目
當(dāng)點(diǎn)D不是AC的中點(diǎn)時(shí)，線段AD CE．（填“＞”，“＜”或“=”）
理由如下：
如圖2，過點(diǎn)D作DF∥BC，交AB于點(diǎn)F．（請你完成后面的解答過程）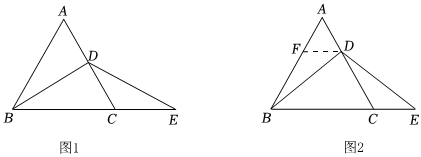
發(fā)布：2025/6/3 7:30:2組卷：13引用：1難度：0.3