2022-2023學年福建省泉州市石獅市八年級（上）期末數(shù)學試卷

一、選擇題（本大題共10小題，每小題4分，共40分）

• 1．下列各數(shù)中是無理數(shù)的是（　　）

  A．0	B．0.1010010001
  C． 3 7	D．π
  組卷：179引用：2難度：0.9

  解析

• 2．4的平方根是（　　）

  A．2

  B．±2

  C．16

  D．±16
  組卷：403引用：1難度：0.8

  解析

• 3．下列運算中正確的是（　　）

  A．a(chǎn)?a=2a

  B．a(chǎn)6÷a2=a3

  C．（a2）3=a6

  D．（3a）2=6a2
  組卷：125引用：2難度：0.8

  解析

• 4．某班共有50名學生，在一次體育抽測中有5人不合格，則不合格學生的頻率為（　　）

  A．0.01

  B．0.1

  C．0.2

  D．0.5
  組卷：363引用：3難度：0.7

  解析

• 5．下列選項中，可以用來說明命題“若|a|＞2，則a＞2”是假命題的反例是（　　）

  A．a(chǎn)=-1

  B．a(chǎn)=-2

  C．a(chǎn)=-3

  D．a(chǎn)=3
  組卷：300引用：7難度：0.7

  解析

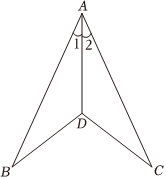• 6．如圖，已知∠1=∠2，則不一定能使△ABD≌△ACD的條件是（　　）

  A．BD=CD

  B．AB=AC

  C．∠B=∠C

  D．∠BDA=∠CDA
  組卷：656引用：15難度：0.9

  解析

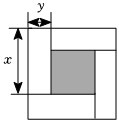• 7．將長、寬分別為x、y的四個完全一樣的長方形，拼成如圖所示的兩個正方形，則這個圖形可以用來解釋的代數(shù)恒等式是（　　）

  A．（x+y）2=x2+2xy+y2	B．（x-y）2=x2-2xy+y2
  C．（x+y）（x-y）=x2-y2	D．（x+y）2-（x-y）2=4xy
  組卷：1571引用：10難度：0.7

  解析

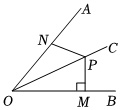• 8．如圖，OC平分∠AOB，點P是射線OC上一點，PM⊥OB于點M，點N是射線OA上的一個動點．若PM=4，則PN的長度不可能是（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：897引用：7難度：0.7

  解析

三、解答題（本題共9小題，共86分）

• 24．已知△ABC≌△DEC，AB=AC，AB＞BC．現(xiàn)將△ABC和△DEC按如圖（1）、圖（2）的方式擺放，連接BD．
  
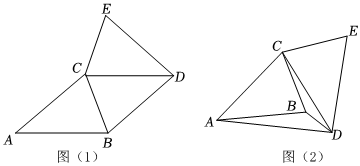
  （1）如圖（1）．
  ①若∠A=40°，請直接寫出∠E的度數(shù)；
  ②若CB平分∠ACD，求證：DB=DC．
  （2）如圖（2），連接AD，若∠BAD=∠BCD，試在線段AD上確定一點M，連接BM，使得△BAM≌△DCB，求∠BMD的度數(shù)．
  組卷：171引用：1難度：0.1

  解析

• 25．在求解一類代數(shù)問題時，我們常常將二次三項式x²+bx+c化成（x+m）²+n的形式，并利用（x+m）²的非負性解決問題．請閱讀下列材料，并解決相關問題：
  【例1】求代數(shù)式x²+4x+7的最小值．
  解：x²+4x+7=x²+4x+4+3=（x+2）²+3．
  因為（x+2）²≥0，所以（x+2）²+3≥3，即代數(shù)式x²+4x+7的最小值為3．
  【例2】若m²-2mn+2n²-8n+16=0，求m、n的值．
  解：因為m²-2mn+2n²-8n+16=0，
  所以（m²-2mn+n²）+（n²-8n+16）=0，
  即（m-n）²+（n-4）²=0，
  因為（m-n）²≥0，（n-4）²≥0，
  所以

  m - n = 0

  n - 4 = 0

  ，
  即m=n=4．
  （1）求代數(shù)式x²+6x+10的最小值；
  （2）在△ABC中，BC=a,AC=b,AB=c.
  ①若△ABC是等腰三角形，且滿足a²-8a+b²-14b+65=0，求△ABC的周長；
  ②若c-b=1，且c（b-25）+2a²-20a+219=0，求△ABC中最大邊上的高．
  組卷：481引用：3難度：0.5

  解析