【經(jīng)典回顧】
梅文鼎是我國(guó)清初著名的數(shù)學(xué)家，他在《勾股舉隅》中給出多種證明勾股定理的方法圖1是其中一種方法的示意圖及部分輔助線．
在△ABC中，∠ACB=90°，四邊形ADEB、ACHI和BFGC分別是以Rt△ABC的三邊為一邊的正方形．延長(zhǎng)IH和FG，交于點(diǎn)L，連接LC并延長(zhǎng)交DE于點(diǎn)J，交AB于點(diǎn)K，延長(zhǎng)DA交IL于點(diǎn)M．
（1）證明：AD=LC；
（2）證明：正方形ACHI的面積等于四邊形ACLM的面積；
（3）請(qǐng)利用（2）中的結(jié)論證明勾股定理．
（4）【遷移拓展】
如圖2，四邊形ACHI和BFGC分別是以△ABC的兩邊為一邊的平行四邊形，探索在AB下方是否存在平行四邊形ADEB，使得該平行四邊形的面積等于平行四邊形ACHI、BFGC的面積之和．若存在，作出滿足條件的平行四邊形ADEB（保留適當(dāng)?shù)淖鲌D痕跡）；若不存在，請(qǐng)說(shuō)明理由．
【考點(diǎn)】四邊形綜合題．
【答案】（1）見(jiàn)解析；
（2）見(jiàn)解析；
（3）見(jiàn)解析；
（4）存在，見(jiàn)解析．
（2）見(jiàn)解析；
（3）見(jiàn)解析；
（4）存在，見(jiàn)解析．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：155引用：3難度：0.1
相似題
-
1．（1）如圖1，在四邊形ABCD中，∠ABC=∠ADC=90°，AD=CD，對(duì)角線BD=8，求四邊形ABCD的面積；
（2）如圖2，園藝設(shè)計(jì)師想在正六邊形草坪一角∠BOC內(nèi)改建一個(gè)小型的兒童游樂(lè)場(chǎng)OMAN．其中OA平分∠BOC，OA=100米，∠BOC=120°，點(diǎn)M，N分別在射線OB和OC上，且∠MAN=90°，為了盡可能的少破壞草坪，要使游樂(lè)場(chǎng)OMAN面積最小，你認(rèn)為園林規(guī)劃局的想法能實(shí)現(xiàn)嗎？若能，請(qǐng)求出游樂(lè)場(chǎng)OMAN面積的最小值；若不能，請(qǐng)說(shuō)明理由．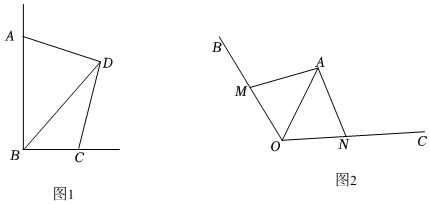
發(fā)布：2025/6/9 15:0:1組卷：243引用：2難度：0.2 -
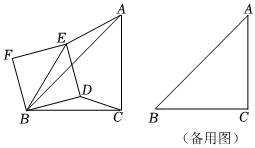2．如圖，在Rt△ABC中，AC=BC=4，∠ACB=90°，正方形BDEF的邊長(zhǎng)為2，將正方形BDEF繞點(diǎn)B旋轉(zhuǎn)一周，連接AE、BE、CD．
（1）請(qǐng)判斷線段AE和CD的數(shù)量關(guān)系，并說(shuō)明理由；
（2）當(dāng)A、E、F三點(diǎn)在同一直線上時(shí)，求CD的長(zhǎng)；
（3）設(shè)AE的中點(diǎn)為M，連接FM，試求線段FM長(zhǎng)的取值范圍．發(fā)布：2025/6/9 15:0:1組卷：209引用：1難度：0.1 -
3．[閱讀理解]
“倍長(zhǎng)中線”是初中數(shù)學(xué)一種重要的思想方法．如圖1，在△ABC中，AD是BC邊上的中線，若延長(zhǎng)AD至E，使DE=AD，連接CE，可根據(jù)SAB證明△ABD≌△ECD，則AB=EC．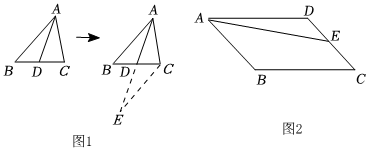
[問(wèn)題提出]
（1）如圖2，平行四邊形ABCD中，點(diǎn)E為CD邊的中點(diǎn)，在BC邊上找一點(diǎn)F，使得AF=AD+CF（要求：用直尺和圓規(guī)作圖，保留作圖痕跡，不寫作法）．
（2）按照你（1）中的作圖過(guò)程證明：AF=AD+CF．發(fā)布：2025/6/9 15:30:2組卷：265引用：3難度：0.1