仔細觀察圖（1）易得∠1=∠2+∠3．依此規律，把圖（1）推廣到圖（2），得到如圖中的8個角：∠1，∠2，…，∠8．若存在這樣的一組正整數x,y,z,滿足2≤x≤y≤z≤8，且使得∠1=∠x+∠y+∠z,那么這組正整數（x,y,z）可以是（　　）

A．（3，4，7）或（4，5，8）	B．（3，5，5）或（3，6，8）
C．（4，4，7）或（3，7，8）	D．（3，3，7）或（2，5，8）

【答案】D

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/5/27 14:0:0組卷：37引用：1難度：0.5

相似題

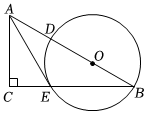1．如圖，在Rt△ACB中，∠C=90°，點O在斜邊AB上，以O為圓心，OB為半徑作⊙O，分別與AB，BC相交于點D，E，連接AE，若AE恰好與⊙O切于點E．
（1）求證：△ACE∽△BCA；
（2）若AC=4，BE=6，求⊙O的半徑．
發布：2025/6/4 17:30:2組卷：295引用：2難度：0.6
解析
2．在如圖的正方形格點紙中，每個小的四邊形都是邊長為1的正方形，A、B、C、D都是格點，AB與CD相交于O，則AO：OB=
．
發布：2025/6/4 14:0:1組卷：1349引用：9難度：0.7
解析
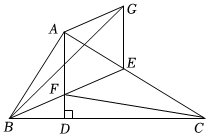3．如圖，在Rt△ABC中，∠BAC=90°，AD⊥BC于點D，E為AC邊上的中點，連接BE交AD于F，將△AFE沿著AC翻折到△AGE，恰好有GE∥AD，連接CF、BG，則下列結論：
①四邊形AFEG為菱形；②S_△ABF=S_△CBF；③2AE²=BD?BC；④
tan
∠
ABG
=
2
5
．
上述結論中正確的有
．（填正確的序號）
發布：2025/6/4 17:0:1組卷：207引用：3難度：0.2
解析

相關試卷

1．如圖，在Rt△ACB中，∠C=90°，點O在斜邊AB上，以O為圓心，OB為半徑作⊙O，分別與AB，BC相交于點D，E，連接AE，若AE恰好與⊙O切于點E．（1）求證：△ACE∽△BCA；（2）若AC=4，BE=6，求⊙O的半徑．