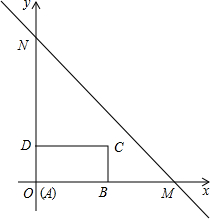
如圖，直線MN：y=-x+b與x軸交于點M（4，0），與y軸交于點N，長方形ABCD的邊AB在x軸上，AB=2，AD=1．長方形ABCD由點A與點O重合的位置開始，以每秒1個單位長度的速度沿x軸正方向做勻速直線運動，當點A與點M重合時停止運動．設長方形運動的時間為t秒，長方形ABCD與△OMN重合部分的面積為S．
（1）求直線MN的解析式；
（2）當t=1時，請判斷點C是否在直線MN上，并說明理由；
（3）請求出當t為何值時，點D在直線MN上；
（4）直接寫出在整個運動過程中S與t的函數關系式．
【考點】一次函數綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：495引用：3難度：0.1
相似題
-
1．如圖1，兩個正方形拼接成一個“L”型的圖形，現用一條直線將圖形分為面積相等的兩部分．小穎在研究時發現了三種不同的分割方法，圖2是其中一種方法．
（1）請在下面圖形（圖5）中再畫出另外兩種分割方法；
（2）若小正方形的邊長為2，大正方形的邊長為4．小穎在利用繪圖軟件研究分割方法時，將圖1放置在平面直角坐標系中，如圖3所示，此時圖2所示的分割直線AB的表達式為y=-x+13．小穎發現：上述三種不同的分割直線都經過同一個點．請你證明此發現；43
（3）小穎繼續研究，又發現了一種分割方法，如圖4所示．請根據此圖，簡述其作圖思路；
（4）通過上述探究過程，談談你的收獲．（兩條即可）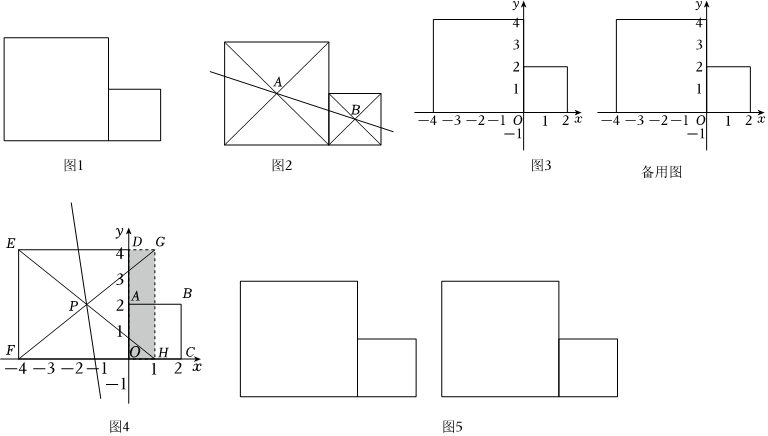
發布：2025/5/21 13:30:2組卷：144引用：2難度：0.3 -
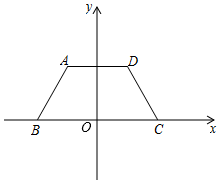2．如圖，在梯形ABCD中，AD∥BC，AB=CD，以邊BC所在直線為x軸，邊BC的中點O為原點建立直角坐標平面，已知點B的坐標為（-4，0），直線AB的解析式為y=2x+m.
（1）求m的值；
（2）求直線CD的解析式；
（3）若點A在第二象限，是否存在梯形ABCD，它的面積為30？若存在，請求出點A的坐標；若不存在，請說明理由．發布：2025/1/21 8:0:1組卷：5引用：0難度：0.3 -
3．在平面直角坐標系xOy中，直線y=kx（k≠0）在x軸及其上方的部分記為射線l.對于定點A（2
，0）和直線y=kx（k≠0），給出如下定義：同時將射線AO和直線y=kx分別繞點A和原點O順時針旋轉α（0°＜α＜180°）得到l1和l2，l1與l2的交點為點P，我們稱點P為射線l的“k-α”雙旋點．如圖，點P為y=2x的“2-30°”雙旋點．3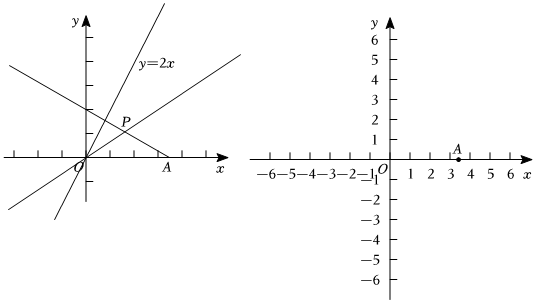
（1）若k=-3
①在給定的平面直角坐標系xOy中，畫出“k-90°”的雙旋點P1；
②直接寫出α=30°的雙旋點P2的坐標 ；
③點P1（1，1）、P2（，3）、P3（0，2）是y=kx的“3”雙旋點的是 ；-3-α
（2）直線y=-2x+4分別交x軸、y軸于點M、N，若存在α，使直線y=kx的“k-α”雙旋點在線段MN上，求k的取值范圍；
（3）當時，對于任意的α，若存在某個三角形上的所有點都是射線y=kx的“k-α”雙旋點，直接寫出這個三角形面積的最大值．-3≤k≤-32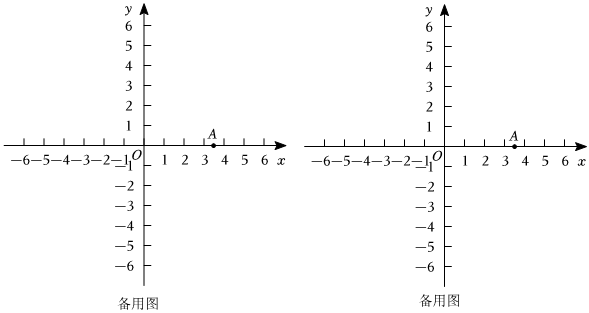
發布：2025/5/21 13:0:1組卷：409引用：1難度：0.3