已知函數f(x)=2cos(ωx+φ)+2(0<ω<2,0<φ<π2).請在下面的三個條件中任選兩個解答問題.①函數f(x)的圖象過點(0,22);②函數f(x)的圖象關于點(12,2)對稱;③函數f(x)相鄰兩個對稱軸之間距離為2.
(1)求函數f(x)的解析式;
(2)當a∈(-2,0)時,是否存在實數a滿足不等式f(2a+32)>f(a)?若存在,求出a的范圍,若不存在,請說明理由.
2
π
2
2
1
2
,
2
3
2
【答案】(1)f(x)=2cos(x+)+.
(2)(-,-).
π
2
π
4
2
(2)(-
3
2
5
6
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/5/7 8:0:9組卷:48引用:3難度:0.4
相似題
-
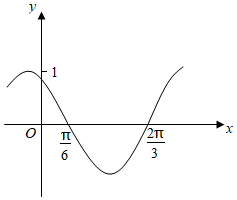 1.如圖是函數y=sin(ωx+φ)的部分圖像,則sin(ωx+φ)=( )
1.如圖是函數y=sin(ωx+φ)的部分圖像,則sin(ωx+φ)=( )A.sin(x+ )π3B.sin( -2x)π3C.cos(2x- )π3D.cos( -2x)5π6發布:2024/12/29 13:0:1組卷:306引用:4難度:0.6 -
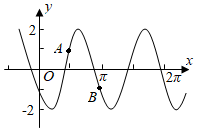 2.已知函數f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分圖象如圖所示,且,則φ值為.A(π2,1),B(π,-1)發布:2024/12/29 13:30:1組卷:147引用:5難度:0.5
2.已知函數f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分圖象如圖所示,且,則φ值為.A(π2,1),B(π,-1)發布:2024/12/29 13:30:1組卷:147引用:5難度:0.5 -
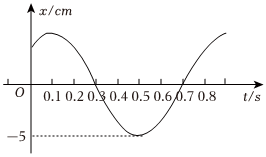 3.如圖所示為一簡諧振動的圖象,則下列判斷正確的是( )
3.如圖所示為一簡諧振動的圖象,則下列判斷正確的是( )A.該質點的振動周期為0.7s B.該質點的振幅為5cm C.該質點在0.1s和0.5s時振動速度最大 D.該質點在0.3s和0.7s時的加速度為零 發布:2025/1/3 11:0:11組卷:26引用:5難度:0.9


