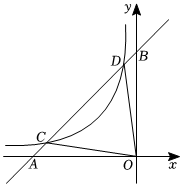
如圖，一次函數y=kx+b（k≠0）與反比例函數y=-6x（x＜0）的圖象交于點C（m,1）和點D（n,6），與坐標軸交于點A，B．
（1）求直線AB的函數表達式．
（2）結合圖象，直接寫出不等式-6x＜kx+b的解集．
（3）連接OC，OD，在直線AB上是否存在一點P，使得S△OBP=S△COD，若存在，求出P點的坐標，若不存在，請說明理由．
y
=
-
6
x
（
x
＜
0
）
-
6
x
＜
kx
+
b
【考點】反比例函數與一次函數的交點問題．
【答案】（1）y=x+7；
（2）-6＜x＜-1；
（3）存在，點P（5，12）或P（-5，2）．
（2）-6＜x＜-1；
（3）存在，點P（5，12）或P（-5，2）．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/4 8:0:9組卷：89引用：3難度：0.6
相似題
-
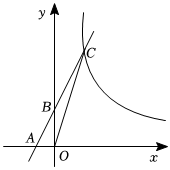1．如圖，在平面直角坐標系xOy中，一次函數y=2x+b的圖象分別與x軸、y軸交于點A、B，與反比例函數的圖象交于點C，連接OC．已知點B（0，4），△BOC的面積是2．y=kx（x＞0）
（1）求b、k的值；
（2）求△AOC的面積．
（3）觀察圖象，直接寫出關于x不等式：的解集．2x+b＞kx（x＞0）發布：2025/5/24 7:30:1組卷：179引用：1難度：0.6 -
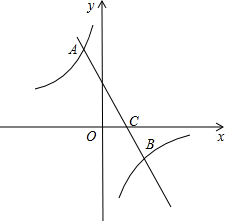2．如圖，直線y=kx+b（k≠0）與雙曲線y=（m≠0）交于點A（-mx，2），B（n,-1）．12
（1）求直線與雙曲線的解析式．
（2）點P在x軸上，如果S△ABP=3，求點P的坐標．發布：2025/5/24 8:0:1組卷：2197引用：19難度：0.3 -
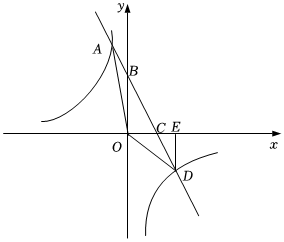3．如圖，直線y=kx+3與x軸、y軸分別交于點B、C，與反比例函數y=交于點A、D，過D作DE⊥x軸于E，連接OA，OD，若A（-2，n），S△OAB：S△ODE=1：2．mx
（1）求反比例函數的表達式；
（2）求點C的坐標；
（3）直接寫出關于x不等式：＞kx+3的解為 ．mx發布：2025/5/24 8:0:1組卷：670引用：3難度：0.7