綜合實踐活動：
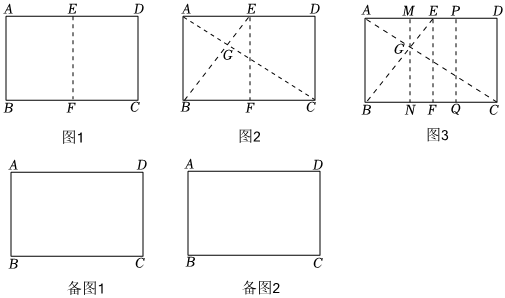
【用數學的眼光觀察】將一張矩形紙片ABCD（如圖1）對折，使AB、DC重合，得到折痕EF（如圖1），把紙片展平，則點F平分邊BC，然后按照如下步驟折疊可使邊BC被三等分．
（1）第一步：在圖1的基礎上，折出AC、BE，將AC與BE的交點記為G（如圖2）．
第二步：過點G折疊紙片，使點A、B分別落在AD、BC邊上的點P、Q處，折痕為MN（如圖3）．把紙片展平，則點N、Q三等分邊BC．根據上述折疊的步驟，在劃橫線處完善折疊研究思路：AE∥BC→AEBC=12→AGCG=12→AMCN=12→BNBC=1313；
【用數學的思維思考】
（2）能否用一種不同于（1）的方法折疊，使BC邊被三等分？請借助于備圖1說明理由；
【用數學的語言表達】
（3）借助（1）中獲得的經驗進行折疊，在備圖2中使用無刻度直尺把BC邊五等分．（直接畫圖即可）
AE
∥
BC
→
AE
BC
=
1
2
→
AG
CG
=
1
2
→
AM
CN
=
1
2
→
BN
BC
1
3
1
3
【考點】相似形綜合題．
【答案】
1
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：154引用：2難度：0.3
相似題
-
1．已知四邊形ABCD中，E、F分別是AB、AD邊上的點，DE與CF交于點G．
問題發現：
（1）①如圖1，若四邊形ABCD是正方形，且DE⊥CF于G，則=；DECF
②如圖2，當四邊形ABCD是矩形時，且DE⊥CF于G，AB=m,AD=n,則=；DECF
拓展研究：
（2）如圖3，若四邊形ABCD是平行四邊形，且∠B+∠EGC=180°時，求證：；DECF=ADCD
解決問題：
（3）如圖4，若BA=BC=5，DA=DC=10，∠BAD=90°，DE⊥CF于G，請直接寫出的值．DECF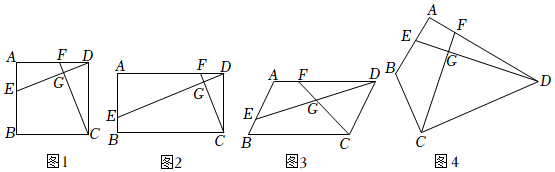
發布：2025/5/23 23:30:1組卷：2292引用：6難度：0.3 -
2．如圖，在矩形ABCD中，tan∠ABD=
，E是邊DC上一動點，F是線段DE延長線上一點，且∠EAF=∠ABD，AF與矩形對角線BD交于點G．34
（1）當點F與點C重合時，如果AD=6，求DE的長；
（2）當點F在線段DC的延長線上，
①求的值；AGAE
②如果DE=3CF，求∠AED的余切值．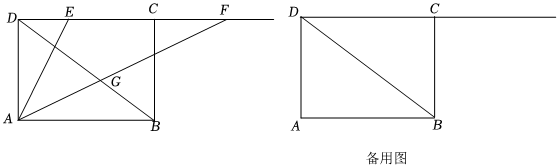
發布：2025/5/24 2:30:1組卷：479引用：1難度：0.2 -
3．[問題情境]
（1）王老師給愛好學習的小明和小穎提出這樣一個問題：如圖①，在△ABC中，AB=AC，P為邊BC上的任一點，過點P作PD⊥AB，PE⊥AC，垂足分別為D，E，過點C作CF⊥AB，垂足為F．求證：PD+PE=CF．
小明的證明思路是：
如圖②，連接AP，由△ABP與△ACP面積之和等于△ABC的面積可以證得：PD+PE=CF．
小穎的證明思路是：
如圖②，過點P作PG⊥CF，垂足為G，可以證得：PD=GF，PE=CG，則PD+PE=CF．
請你選擇小明、小穎兩種證明思路中的任意一種，寫出詳細的證明過程．
[變式探究]（2）如圖③，當點P在BC延長線上時，問題情境中，其余條件不變，求證：PD-PE=CF．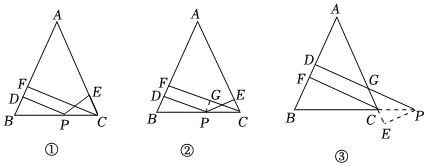
[結論運用]（3）如圖④，將矩形ABCD沿EF折疊，使點D落在點B上，點C落在點C'處，點P為折痕EF上的任一點，過點P作PG⊥BE，PH⊥BG，垂足分別為G，H，若AD=8，CF=3，求PG+PH的值．
[遷移拓展]（4）圖⑤是一個機器模型的截面示意圖，在四邊形ABCD中，E為AB邊上的一點，ED⊥AD，EC⊥CB，垂足分別為D，C，且AD?CE=DE?BC，AB=2cm,AD=3cm,BD=13cm,MN分別為AE，BE的中點，連接DM，CN，請直接寫出△DEM與△CEN的周長之和．37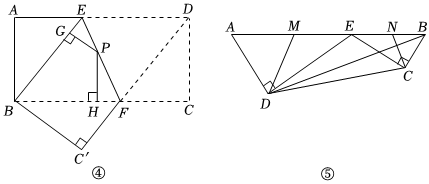
發布：2025/5/24 0:30:1組卷：278引用：1難度：0.1
相關試卷