如圖，在平面直角坐標系中，拋物線y=ax2+bx+3（a≠0）與y軸交于點C，與x軸交于A，B兩點（點A在點B的左側），且A點坐標為（-5，0），拋物線的對稱軸為直線x=-2．
（1）求拋物線的解析式；
（2）點M是位于直線AC上方的拋物線上任意一點，過點M作MP∥x軸交直線AC于點P，過點P作PN∥BC交x軸于點N．求PM+104PN的最大值及此時點M的坐標；
（3）將原拋物線沿射線CB方向平移10個單位后得到新拋物線y'，E為新拋物線y'的對稱軸上一點，F為新拋物線y'上一點，若以點C、E、F為頂點的三角形是以CE為腰的等腰直角三角形，請直接寫出點E的坐標，并把求其中一個點E的坐標的過程寫出來．
10
4
10
【考點】二次函數綜合題．
【答案】（1）；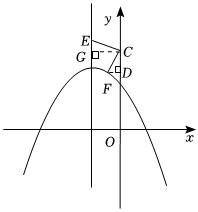
（2）最大值，此時點M的坐標為；
（3）或或（-1，）或（-1，1）．
y
=
-
3
5
x
2
-
12
5
x
+
3
（2）
PM
+
10
4
PN
32
3
（
-
7
3
，
16
3
）
（3）
E
（
-
1
，
4
-
6
3
）
E
（
-
1
，
4
+
6
3
）
10
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/7 1:0:8組卷：438引用：2難度：0.2
相似題
-
1．如圖，在平面直角坐標系中，矩形OABC的頂點A和C分別在y軸的正半軸和x軸的正半軸上，OA=8，OC=10．拋物線y=-
x2+bx+c與y軸交于點A，與BC邊交于點D．將矩形OABC沿直線AD折疊，點B恰好落在x軸上的點E處．14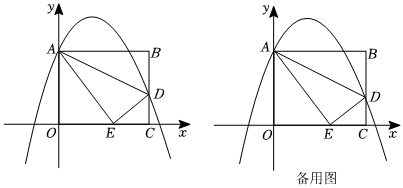
（1）點E的坐標為 ，點D的坐標為 ；
（2）求拋物線的函數表達式；
（3）點F為拋物線上一動點（點F不與點A、D重合），設F點的橫坐標為m.
①若點F在AD上方的拋物線上，連接AF、DF，設△ADF的面積為S，求S與m的函數關系式，并求S的最大值．
②該拋物線上是否存在一點F，使得直線EF恰好可以把△ADE分成面積之比為2：3的兩部分？如果存在，請直接寫出m的值；如果不存在，請說明理由．發布：2025/5/24 23:30:2組卷：168引用：1難度：0.4 -
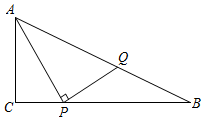2．如圖，Rt△ABC中，∠C=90°，P是CB邊上一動點，連接AP，作PQ⊥AP交AB于Q．已知AC=3cm,BC=6cm,設PC的長度為x cm,BQ的長度為y cm.
小青同學根據學習函數的經驗對函數y隨自變量x的變化而變化的規律進行了探究．
下面是小青同學的探究過程，請補充完整：
（1）按照下表中自變量x的值進行取點、畫圖、測量，分別得到了y的幾組對應值；
（說明：補全表格時，相關數據保留一位小數）x/cm 0 0.5 1.0 1.5 2.0 2.5 3 3.5 4 4.5 5 6 y/cm 0 1.56 2.24 2.51 m 2.45 2.24 1.96 1.63 1.26 0.86 0
m的值約為 cm；
（2）在平面直角坐標系中，描出以補全后的表格中各組數值所對應的點（x,y），畫出該函數的圖象；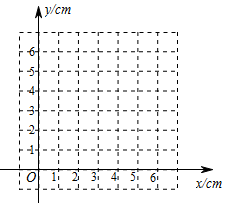
（3）結合畫出的函數圖象，解決問題：
①當y＞2時，對應的x的取值范圍約是 ；
②若點P不與B，C兩點重合，是否存在點P，使得BQ=BP？（填“存在”或“不存在”）發布：2025/5/24 23:0:1組卷：561引用：6難度：0.4 -
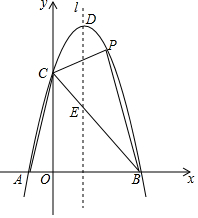3．如圖，拋物線y=ax2+bx+8（a≠0）與x軸交于點A（-2，0）和點B（8，0），與y軸交于點C，頂點為D，連接AC，BC，BC與拋物線的對稱軸l交于點E．
（1）求拋物線的表達式；
（2）點P是第一象限內拋物線上的動點，連接PB，PC，當S△PBC=S△ABC時，求點P的坐標；35
（3）點N是對稱軸l右側拋物線上的動點，在射線ED上是否存在點M，使得以點M，N，E為頂點的三角形與△OBC相似？若存在，求點M的坐標；若不存在，請說明理由．發布：2025/5/25 0:30:1組卷：4953引用：13難度：0.3