根據以下素材,探索完成任務.
| 如何設計拱橋景觀燈的懸掛方案? | ||
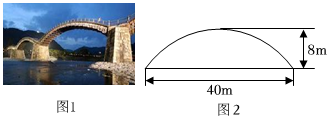
| 素材1 | 圖1中有一座拱橋,圖2是其拋物線形橋拱的示意圖,某時測得水面寬40m,拱頂離水面8m.據調查,該河段水位在此基礎上再漲2.1m達到最高. |
|
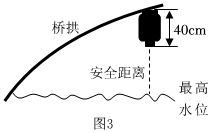
| 素材2 | 為迎佳節,擬在圖1橋洞前面的橋拱上懸掛40cm長的燈籠,如圖3.為了安全,燈籠底部距離水面不小于1m;為了實效,相鄰兩盞燈籠懸掛點的水平間距均為1.6m;為了美觀,要求在符合條件處都掛上燈籠,且掛滿后成軸對稱分布. |
|
| 問題解決 | ||
| 任務1 | 確定橋拱形狀 | 在圖2中建立合適的直角坐標系,求拋物線的函數表達式. |
| 任務2 | 探究懸掛范圍 | 在你所建立的坐標系中,僅在安全的條件下,確定懸掛點的縱坐標的最小值和橫坐標的取值范圍. |
| 任務3 | 擬定設計方案 | 給出一種符合所有懸掛條件的燈籠數量,并根據你所建立的坐標系,求出最左邊一盞燈籠懸掛點的橫坐標. |
【考點】二次函數的應用;坐標與圖形變化-對稱.
【答案】任務1:y=-;
任務2:懸掛點的縱坐標的最小值是-4.5,懸掛點的橫坐標的取值范圍是-15≤x≤15;
任務3:方案一:從頂點處開始懸掛燈籠,19盞燈籠,最左邊一盞燈籠懸掛點的橫坐標是-14.4;方案二:從對稱軸兩側開始懸掛燈籠,共可掛18盞燈籠,最左邊一盞燈籠懸掛點的橫坐標是-13.6.(答出一種方案即可).
1
50
x
2
任務2:懸掛點的縱坐標的最小值是-4.5,懸掛點的橫坐標的取值范圍是-15≤x≤15;
任務3:方案一:從頂點處開始懸掛燈籠,19盞燈籠,最左邊一盞燈籠懸掛點的橫坐標是-14.4;方案二:從對稱軸兩側開始懸掛燈籠,共可掛18盞燈籠,最左邊一盞燈籠懸掛點的橫坐標是-13.6.(答出一種方案即可).
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/31 2:0:7組卷:729引用:3難度:0.6
相似題
-
1.某商品的進價為每件33元,現在的售價為每件60元,每星期可賣出300件.市場調查反映,如果調整商品售價,每降價1元,每星期可多賣出20件.
(1)商場要想平均每星期盈利8500元,每件商品的售價應為多少元?
(2)商場要想平均每星期獲得最大利潤,每件商品的售價應為多少元?發布:2025/6/1 9:30:1組卷:10引用:2難度:0.7 -
2.某商品現在的售價為每件60元,每星期可賣出300件,市場調查反映:如調整價格,每漲價1元,每星期要少賣出10件;每降價1元,每星期可多賣出20件,已知商品的進價為每件40元,如何定價才能使利潤最大.
發布:2025/6/1 9:0:1組卷:1037引用:12難度:0.5 -
3.疫情防控期間網絡訂餐實施“零接觸”配送,德清縣某快餐店配送某種套餐,每份套餐的成本價為30元.該快餐店店主結合訂單數據發現,日銷售量y(份)是每份套餐售價x(元)的一次函數,其中x,y的四組對應值如表:
另外,該快餐店每日固定支出費用為1800元(不含套餐成本).每份套餐售價x(元) 35 40 45 50 日銷售量y(份) 350 300 250 200
注:日凈收入=日銷售量×(每份套餐售價-每份套餐成本價)-每日固定支出.
(1)求日銷售量y關于每份套餐的售價x的函數關系式(不要求寫出自變量的取值范圍);
(2)若日凈收入為W(元),求出W與x的函數關系式;
(3)當每份套餐的售價定為多少元時,日凈收入最大,最大日凈收入是多少?發布:2025/6/1 9:30:1組卷:13引用:1難度:0.5


